《因数与倍数》练习             

一、活用概念，准确填空。

1．48的因数有（                   ），其中奇数有（    ）个，偶数有（   ）个，质数有（      ）个，合数有（     ）个。

2．一个两位数，个位是最小的合数，十位上是3的倍数，这个数最大是（     ）。

3．m、12、y是三个连续自然数，和是（      ）。

4．如果a、b、c是不等于0和1的自然数，A=a×b×c，那么A至少有（     　）个因数。

5．用0、1、2三个数字组成的所有三位数中，同时是2、3、5的倍数的数有（    　）和（       ）。

6．在每组数后面的（    ）里写上最大公因数，在[    ]里写上最小公倍数。

24和6 （    ） [     ]            24和18 （    ）  [     ]

4和13 （    ） [     ]            39和26 （    ）  [     ]

7．一个数是3的倍数，又是5的倍数，还有因数7。这个数最小是（　　　　　）。

8．1082至少加上（　　　）是3的倍数，至少减去（　　　）才是5的倍数。

9．如果a+1=b，那么a与b的最大公因数是（　     ），最小公倍数是（　   　）；如果a=b÷3，那么它们的最大公因数是（        ），最小公倍数是（　  　　）。

10.五（1）班学生分组进行综合实践活动，每组12人或每组16人都正好分完，五(1) 班最少有(      )名学生；

五（2）班学生每组10人或每组15人都剩1人，五（2）班最少有(     )名学生；

五（3）班学生每组10人或每组12人都缺2人，五（3）班最少有(     )名学生。

11.两个连续偶数的和是30，这两个偶数分别是（      ）和（      ），它们的最大公因数是（      ），最小公倍数是（      ）。

★12.如果A=2×3×5，B=2×2×5，那么A和B的最大公因数是（      ），最小公倍数是（       ）。

二、反复比较，精挑细选。（选择正确答案的序号填入括号中。）

1．任何两个自然数的（  　 ）的个数是无限的。

A．公倍数           B．公因数       　    C．倍数

2．方程2.4 x－0.4x＝4的解与方程（  　 ）的解相同。

A．4 x－1.2＝3.8     B．4.5 x＋1.5x＝12    C．0.3 x－0.1x＝0.5

3．x÷y＝6……11中，其中y最小可以是（  　 ），这时x是（  　 ）。

A．0； 11      　    B．1；  17           C．12； 83

4．两个数的最大公因数是15，最小公倍数是90，这两个数一定不是（  　 ）。

A．15和90           B．45和90           C．45和30

5．一个长方形长ɑ米，宽8米，这个长方形的周长不可以表示成（  　 ）。

A．2（ɑ＋8）         B．8ɑ                C．2ɑ＋16

三、仔细审题，细心计算。

1．解方程。

x－162＝189              3x＋2.7＝5.94               8x－x=14.7

 

 

 

 

0.58＋x—0.69＝0.95         2.6x－0.44×2＝1.2          2x＋0.4x=48

 

 

 

 

2．看图列式方程，并解答。

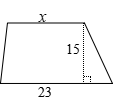
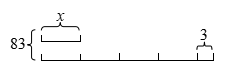① 梯形的面积为300平方米。（单位：米）    ②

 

 

 

 

 

 

四、走进生活，解决问题。（1～3题列方程解决）

1．为绿化城市，市政公司四月份投放花草3800盆，比三月份的4倍还多200盆，三月份投放花草多少盆？

 

 

 

 

2．新乡中学买了同样多的篮球和排球，买排球比篮球一共少用42元，每个篮球48.5元，每个排球45.7元。篮球、排球各买了多少个？

 

 

 

 

 

3．爸爸：“今天中午做什么饭？”

妈妈：“酸菜鱼，看，这是我刚买的1条鱼和2包酸菜。”

爸爸:“这条鱼真大！有多重？”

下面妈妈提供一些信息：

 

 

 

 

 

 

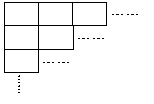4．用长5厘米、宽4厘米的长方形，照右图的样子拼

   成正方形。拼成的正方形的边长最小是多少厘米？

   需要几个长方形？

 

 

 

 

5．有35个苹果和34个梨，平均分给舞蹈队的小

   朋友，结果苹果多了3个，梨少了6个。舞蹈

   队有多少个小朋友？

 

 

 

 

6．长途汽车站每15分钟向南京发一次车，每20分钟向常州发一次车，6:00同时发车后，要到什么时间会再次同时发车？

 

 

 

 

7．一种彩纸长30厘米，宽18厘米，要用它拼成一个正方形写字栏，这个写字栏的面积最小是多少？

 

 

 

 

8．园林工人在长48米的小路两边每隔6米栽一棵树（首尾都栽），现在要改成每隔4米栽一棵树，那么不用移栽的树有多少棵？

 

 

 

 

9．一条道路AC的中间有一个石凳B，已知AB长630m，BC长540m。要求在A到C中间等距离的安装落地灯，且A、B、C处都要安装，这条道路上至少有多少盏落地灯？

 

 

 

 

★★拓展：

1．一个长方形的池塘，如果在它的四周及四角栽上风景

树，每相邻两棵树之间的距离要相等，那么最多每几

米栽一棵？需要栽多少棵？

 

 

 

 

2．在一根长100cm的木棍上（两端都不点），自左向右每隔6cm染一个红点，同时自右向左每隔5cm染一个蓝点，有多少个点同时染上红色和蓝色？