分数乘整数

【教学目标】

1. 使学生结合具体问题的数量关系主动把整数乘法的意义推广到分数乘法，理解分数乘整数的算理，掌握算法，感悟整数、小数、分数乘法运算的一致性，能运用分数乘整数解决一些简单实际问题。

2.使学生在推广乘法意义、探索分数乘整数的算理与算法、用所学计算解决实际问题的过程中发展几何直观、推理意识，以及分析和解决问题能力。

3. 使学生在探索算法的过程中进一步感受数学与生活的关联，感悟数学的价值，逐步养成独立思考、细心计算的习惯，增强对数学学习的自信心。

【教学难重点】

探索分数乘整数的算理与算法，在整体关联中感悟乘法运算的一致性。

【教学内容】

一、导入新知，建构意义

师：六年级一班的王晓星同学打算做一些小礼物送给他的好朋友。让我们一起走进他的手工课堂吧。

王晓星：我要做3把彩虹伞，需用多少张卡纸？

提问：为什么用乘法计算，也可以用加法计算？

王晓星：做3束捧花，需要多少根扭扭棒？ （并说一说这么列式的道理。）

王晓星：扎染3块手帕，要用多少克颜料？（并说一说这么列式的道理。） 

王晓星：我还想做一些绸花，做1朵绸花要用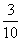米绸带。做3朵这样的绸花， 一共要用几分之几米绸带？

提问：这里的米表示什么意思？如果用长方形直条表示1米的绸带，你准备怎样涂色？

课件出示：

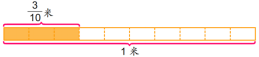
提问：做三朵绸花要用多长的绸带？你会列式吗？

预设：①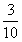×3 ②++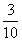

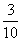提问：你是怎样想到用乘法列式的？

引导：求3个的和，也可以用乘法计算。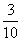×3就表示——生：（齐）3个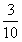相加。

揭题：可见，分数乘整数的意义与整数乘法的意义相同，都是求几个相同加数的和是多少。今天开始我们将一起进入分数乘法的世界。今天学习第一课：分数乘整数（板书课题）。

追问：那这样的乘法算式该怎么算呢？

【设计意图】引入新知，建构意义课前，课始设计王晓星同学手工课堂的大情境，引出整数乘法、小数乘法和分数乘法。从学生熟悉的整数、小数乘法引入，可以让他们自然而然地体会到分数乘整数的意义在本质上与整数乘法的意义相同，都是求几个相同加数和的简便运算。在潜移默化中，不露痕迹地把整数乘法的意义推广到分数中来，能使学生对乘法运算的意义有一个结构化的认识和理解。同时，通过对整数乘法和小数乘法计算方法的求同，实现关联统一，即计算结果都是对计数单位个数的表达，为后面探究分数乘法提供思维支撑。这样教学，有利于学生感受运算意义的一致性。

二、多元表征，理解算理，建构算法

1.探究分数乘整数的算理。

（1）下面请大家利用已有的经验想一想、算一算，再把你的想法记录在作业纸上。

（2）收集学生的回答情况，组织全班展示交流。

投影作品展示。

预设：展示作品①

提问：你能看懂他的方法吗？谁愿意来说一说？

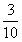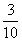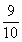预设1：×3就是求3个相加的和， 他是先在图上画出3个，在通过数一数得到有9个，所以是米。

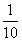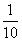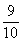预设2：做一朵绸花需要3个米，做3朵绸花就要9个米，也就是米。

过渡：怎样通过计算的方法得出是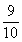米呢？我们一起看一看。

展示作品②

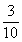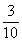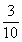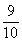×3=++=（米）

提问：谁能来说一说这位同学是怎样计算的？

预设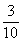：×3表示3个相加，先转化成加法，就可以用我们以前学过的知识来解决了。

展示作品③

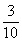×3=0.3×3=0.9=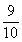

预设：他是根据小数的意义来思考的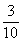，可以表示成0.3，3个0.1乘3就是0.9。

展示作品④

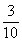×3==

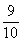
提问：为什么直接用分子与整数相乘的积做分子？

预设：里有3个，3个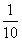乘3就是9个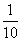，也就是。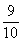

引导：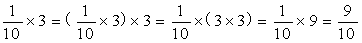

提问：仔细观察，这么多方法都指向同一个相同点，你能找到吗？

总结：是的，不论是画图、转化，还是直接计算，都是计算分数单位的个数。

2、构建算法。

选择自己喜欢的方法计算。

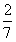×3=

学生交流分享。

提问：想一想，分子“6”是怎样得到？

追问：怎样理解这里的“2×3”？

引导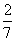：×3=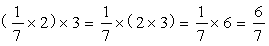

指出：理解了分数乘整数的算理，以后计算时就可以直接”用分子与整数相乘的积作分子，分母不变。”来算了。

提问：你能用一句话说一说分数乘整数可以怎样计算吗？

追问：分母不变，也就是——？分数的分子与整数相乘的积，就是再算？

【设计意图】方法的获得必须要经历自主探索的过程。对于相同的问题，不同的学生可以有不同的经验、不同的思考。在研究十分之三乘三应该如何计算时这一环节时，放手让学生通过自主尝试探索分数乘整数的算理与算法。结果学生通过画图、分数化小数、根据计算单位思考、用加法算乘法等不同的方法算出了得数。在充分交流的基础上，引导学生通过比较感受不同算法之间的关联，并归纳出分数乘整数的计算方法。启发学生从计数单位个数的角度展开分析与思 考 ，继而理解其中的道理，帮助他们理解算法、掌握算法，发展运算能力和推理意识。整个学习过程展现了学生真实的思考过程，留下了原生态的思维痕迹，学生学习的自主性得以凸显。

3. 完善算法

做一朵绸花要用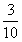米绸带，王晓星做5朵这样的绸花，一共要用绸带几分之几米？

 

同学独立完成解答，然后组织交流反馈。

预设：（1）.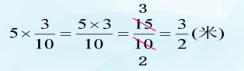

（2）

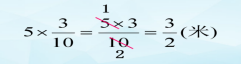
比较：比较上面两种计算过程，你有什么发现？

交流发现：方法一是先计算在约分，方法二是先约分再计算。相比较而言，方法二更简便些。

小结：是啊，计算分数乘整数时，可以先约分再计算。

提问：现在，你能说一说，分数乘整数，我们是怎样计算的？

三、关注本质，把握一致性。

师：想一想，分数乘整数和整数乘整数、小数乘整数在计算上有什么相同的地方？回到开始的算式，现在你有什么新发现？

小结：这几道题都是用3个计数单位与3相乘，得到的结果都是9个这样的计数单位。也就是说都是关于计数单位的运算，在本质上是一样的。

【设计意图】关联统一，整体建构在充分理解了分数乘整数的计算方法之后把分数乘整数的计算置于乘法计算的整体框架之下，以“分数乘整数与整数乘整数、小数乘整数在计算的道理上有什么相同的地方”为核心问题，引导学生结合 实例理解分数乘整数与整数乘整数、小数 乘整数之间相同和不同的地方，并透过现 象看本质，主动发现不同运算之间的内在 联系，感受数的运算在本质上的一致性，从而在整体上理解运算的算理与算法。帮助学生理解乘法的本质的一致性。

三、多样练习，拓展提升。

1.涂一涂，算一算。

学生独立完成涂色操作并列式计算，然后组织反馈。

②看图示变化，写出算式并说一说算式表示的意思。

 比较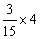和。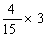

（2）解决实际问题

          ①下面我们一起来解决一个实际问题。学生独立完成幼儿园有36个小朋友，每个小朋友吃块月饼，一共吃多少块月饼?

师：像这样，求几个几分之几是多少的实际问题，可以用乘法计算。

②小红和爸爸一起吃一块月饼，小红吃了这个月饼的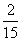 ，爸爸吃的月饼是小红的6倍。爸爸吃了多少个月饼？

交流反馈：×6既可以表示6个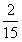是多少，也可以表示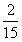的6倍是多少。

师：用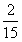×6这道算式还可以解决生活中的哪些问题呢？先独立编一个实际问题，再与小组同学交流。

四、收获体会。