多边形的面积（整理与练习）

【教学内容】

苏教版义务教育教科书《数学》五年级上册第25～26页整理与练习的“回顾与整理”和“练习与应用”第1～5题。

【教学目标】

1.使学生通过回顾与整理，进一步理解和掌握平行四边形、三角形、梯形的面积公式及相互关系，能应用公式计算图形的面积，解决简单的实际问题。

2.使学生掌握面积计算公式的推导方法、过程和相互之间的联系，进一步体验转化思想和模型思想，建构面积计算的知识体系；发展几何直观，并提高应用所学知识解决简单实际问题的能力。

3.使学生体会数学的表达形式，感受数学知识内在联系紧密的特点；逐步形成整理知识、寻找知识联系的意识和学习习惯，逐步培养创新意识。

【教学重点】

整理和认识知识的联系和结构。

【教学准备】

师：课件、平面图形各1个、贴板

生：练习纸

【教学过程】

一、揭示课题

师：同学们，刚刚这个单元，我们主要学习了什么内容？---（多边形的面积）

师：都说温故而知新，今天我们一起对所学过的多边形的面积做一个回顾和整理，好吗？--出示课题

二、整理知识

师：想一想，我们已经知道了哪些多边形的面积？（根据回答贴板呈现）在三年级的时候，我们通过摆1平方厘米的小正方形，归纳推导出了长方形的面积公式，是？---（长方形面积=长×宽）

师:那其余几个图形的面积公式是什么，又是怎样推导出来的呢？请同学们先静下心来想一想，然后选一个图形，和同桌说一说它的面积推导过程。（指3生分别回答，说明公式及推导过程（尽可能详细），教师相机点拨，并完善板书）

师：真好，同学们都是学习的有心人。从交流中我们可以体会到，这些图形的面积推导过程是有一定的顺序和联系的，那谁能上来把这些图形摆一摆，用箭头画一画，整理、表示出它们之间的联系呢？（指1生上台交流摆法）—指向“长方形面积公式是推导其他多边形面积公式的基础”

师：在探究多边形面积计算的过程中，有什么给你留下深刻印象的吗？--指向“转化”思想，指出转化思想将未知的、不熟悉的知识，转化成了已知的、熟悉的知识，将知识紧密的联系在了一起。

师：你能举例说说谁转化成了谁吗？（三角形、梯形通过转化变成了——平行四边形，平行四边形又是通过转化变成——长方形。）所以我们来看，根据转化的过程，这些图形还可以用这样的箭头来整理。（完善板书上的双向箭头）（若在交流摆法时，已经有学生提出按照转化来摆放图形和画箭头，直接完善板书的双向箭头）

师：图形之间还有怎样紧密的联系呢？

（配合课件）我们来观察这样一个梯形，如果我们将它的上底缩短到两个端点重合，这时候，梯形上底变成—（0）；是什么图形？—（三角形）；面积公式就可以写成（指1生）—（S=a×h÷2）。

（配合课件）如果把上底延长到和下底一样长，这时候又是什么图形？怎样计算面积呢？（ 指1生）（上底和下底一样长，就是两个底，底×2和÷2相互抵消，就变成S=a×h）

指出：数学真的有趣又神奇！三角形、平行四边形虽然都不是梯形，但也能仿照梯形面积公式来计算。

三、知识应用

1.基本练习：运用公式直接计算面积（“练习与应用”第2题：计算图形面积）

师：相信大家对图形的面积公式一定烂熟于心了，我们趁热打铁。请同学们拿出练习纸，完成第一题。（指3生交流过程和方法，相机呈现答案）

师：回顾刚刚的解题过程，你觉得在利用公式计算面积时，需要注意什么？

（1）必须找到的是一组对应（合适、匹配）的底和高

（2）三角形、梯形面积公式需要÷2（可追问为什么？没有÷2时，算的是等底等高的平行四边形面积）

（3）注意单位

2.对比练习：突出底、高与面积的关系

（1）“练习与应用”第1题：点子图

师：同学们做题非常细心！（出示题目2）那么这道题目呢？在练习纸上动手试一试！

交流：这4个图形的面积有什么关系？

（利用公式比较图形面积）

第一位学生（投影作业纸）：利用面积公式，计算出4个图形的面积，从而比较出它们的关系；（长方形面积与长方形面积相等；三角形面积与梯形面积相等；它们是2倍关系）（给予肯定）

（利用等底等高关系比较图形面积）

师：有没有同学不需要计算也能比较图形之间的关系？

剩余学生：紧紧抓住底和高的关系：

第一组：长方形和平行四边形等底等高，面积相等；

第二组：三角形和梯形等底等高，面积相等；

第三组：长方形（或平行四边形）和三角形、梯形等底等高，面积则是2倍关系。

    （若在交流过程中，学生指出将平行四边形切拼、两个三角形或梯形组合，引导学生说到图形之间关系为等底等高）

（探究等底等面积、等高等面积情况）

师：同学们的方法真巧妙。利用等底等高也能快速比较出图形的面积关系

师：（点子图中着重出平行四边形和三角形）我们继续深入研究，（指1生读题）

如果现在我想要三角形和平行四边形面积相同，又不改变三角形底的长度，你觉得三角形的高要变成多少呢？（指1生）或在不改变三角形高的长度，三角形的底要变成多少呢？（指1生）

师：谁来小结一下，刚刚我们通过哪些方法来研究图形之间的面积关系？

指出：除了利用公式计算出面积，还可以巧妙的利用图形底、高、面积之间的关系，快速得到答案。

（2）“练习与应用”第3题：画面积相等的图形

师：这些多边形，我们算了算、比了比，现在一起来画一画吧！

出示格子图中的长方形，

师：我们先来观察格子图中的长方形，你了解到什么？（长、宽、面积）

提问：你会画一个和它面积相等的平行四边形吗？动手画一画。

学生交流讨论。（每个层次尽量找多组不同）

（第一层次：利用公式推出底和高乘积）

师：（展示多组）先来快速判断这些同学画的对不对？

师：这些平行四边形形状各不相同，为什么都和长方形面积相等呢？

引导学生回答，利用面积公式，画出的平行四边形底和高的乘积是15，即正确。

师：快通过计算的方法，快速检查一下自己画的是否正确。

（第二层次：利用等底等高的关系）

（最好找到一位同学，画了多个等底等高平行四边形，请他上台交流）

师：樊老师还找到了一位同学，请他来交流交流如何画的。

指出：只要画出来的平行四边形和长方形等底等高，面积就相等。

师：哦！原来画图形，不光可以根据面积公式推出底和高的乘积；还可以利用一些特殊的关系，快速画出图形！

师：那三角形和梯形你能试着画一画吗？

【三角形】

（第一层次：利用公式推出底和高乘积）

师：咱们先来看三角形，如果利用公式推导，三角形底和高乘积得是多少？

生：学生说出底和高乘积必须是30；

（第二层次：利用等底等面积、等高等面积的关系）

师：又有谁是通过特殊关系画出来的？

生：等底等面积：三角形高是2倍；等高等面积：三角形底是2倍。

【梯形】（参照三角形，快速交流，不投影）

师：梯形也可以参照这样的两种方法。

 

师：同桌相互检查一下画的图形是否正确。

 

3、巩固练习：解决实际问题

（1）“练习与应用”第4题

师：在我们生活中，其实有很多和面积计算有关的实际问题，我们一起来看一看。

（出示第四题，让学生独立读题、解答）

投影学生作品，交流两种做法：（注意单位换算）

第一种：先计算出一面小旗的面积，再乘10；

第二种：将两面直角三角形小旗拼成一个长方形，此时10面小旗就转化成了5个长方形，题目所求就变成5个长20厘米、宽12厘米的长方形面积。

点评第二种：这个同学特别善于发现，运用转化的思想也能解决这个实际问题。

师：大家快速检查一下完成的是否正确。

（2）“练习与应用”第5题

师：谁来读题？有困难吗？在练习纸上尝试完成

（选取错误同学答案：未×1投影）

重点交流：“每平方米需用油1千克”需要乘1

 

4、 发散性练习：利用多种思路求面积：

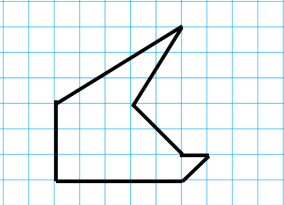
师：解决了生活中的实际问题，我们再来看一个图形，这个图形看起来可有点复杂，你们有办法求出它的面积吗？

选取三位学生作业纸，投影交流三种方法：

第一种方法：数方格；（若无学生用此方法，老师快速点一下）

若有学生，点评：数出来了吗？有没有同学用别的方法来检验一下他数的对不对？

第二种方法：（上台交流）利用分割法，将这个复杂图形转化成了几个简单图形面积之和；

第三种方法：转化（请这位同学上台交流）运用两次等底等高的关系，将图形转化成三角形。

第三种方法可适当引导学生：老师展示：转化下面这个小三角形，利用了等底等高关系，并没有改变面积，师：接下来，你还会用这样的方法继续将这个图形变一变吗？

    比较：比较用不同的方法计算的结果，你有什么想法？

    指出：数学真神奇！看起来形状不同的图形，其实也有非常紧密的联系，只要你在学习中用心体会，一定会有更多的收获。

四、总结、作业

1.课堂总结

师：通过今天的整理与练习，你对本单元的知识、方法又有了哪些新的收获和体会？

2.课后思考

师：我们把目光再次聚焦在黑板，在利用转化思想推导三角形和梯形面积公式时，我们用了两个完全一样的图形，那一个图形可以吗？（出示问题，指生读题）这是留给大家课后完成的思维冲浪题。有兴趣的同学可以课后相互交流交流，好吗？今天的课就上到这里。