引领回顾 建构认知

                    ——江苏省宜兴市第二实验小学   何锦婷

    学生数学知识形成的过程是什么？它不是一个被动吸收、机械记忆、反复练习、强化储存的过程。它是以一种积极的心态，调动原有的知识和经验尝试解决新问题，同化新知识的一个有意义的过程。只有这样，新知识才能纳入原有的认知结构之中，才可能成为有效的知识。

    皮亚杰曾经说：“数学是对结构的建构而建立起来的”。学生在学习一个新知识以前，总有一个完整的知识结构和经验结构，在这种结构中，存在着与新知识相似或者相近的旧知或经验，这些旧知或经验是新知获得意义的“支撑点”，围绕“支撑点”进行一系列的操作、推理、抽象、概括、具体化，使经验上升为理性的知识，使新旧知识之间相互作用。最终形成一个完整的知识结构，这样新知也就纳入了旧知或经验系统而获得意义。可以是新知识的复习引入，新知后的总结延续，对一个知识体的整理与复习达到目的。

一、引导旧知回顾 支撑新知生长

   小学数学的编排结构中，往往后续新知就是以先前的旧知作为学习的起点，作为新知的生长点从而展开的。

实录一：除数是小数的除法（片段）

师：同学们，我们来做一组填空，说说你是怎样想的。（大屏幕）

①1250÷250 =（      ）÷25               ③0.48÷2.4=（      ）÷24

②8÷0.5 =（      ）÷（0.5×2）       ④1.6÷0.04 =（      ）÷4

生1:1250÷250 =（125）÷25，根据商不变的规律：被除数和除数同时乘或除以相同的数（0除外），商不变。

师：真棒！过去学过的商不变的规律，还记得，我们一起说一遍。

生2：除数0.5×2，根据商不变的规律，被除数也要同时乘2，填16。

师：有道理吗？（得到肯定回答后，继续）大家是否发现商不变的规律同样适用在小数除法里？

生3：除数2.4变化成了24，小数点向右移动了一位，乘10，被除数0.48的小数点也必须向右移动一位变成4.8，也乘10。

师追问：为什么不把0.48变成48呢？

生3：变成48就乘了100，商就变了。

师：听明白了吗？移动相同位数，就代表乘相同的数，否则商就变了。

生4: 1.6÷0.04=（160）÷4，被除数和除数同时乘100，也就是小数点同时向右移动两位。1.6小数位数只有一位，再补一个0，小数点也就向右移动了两位。

师：通过这组练习，你发现了什么？

生5: 商不变的规律不但适用于整数除法，小数除法同样适用。

师：现在我们一起来帮妈妈解决一个生活中的问题，可以吗？

出示例10

鸡蛋4.2元/千克，妈妈买鸡蛋用去7.98元。妈妈买了多少千克鸡蛋？

师：你会列式吗？试一试。

生5:问题是求买鸡蛋多少千克？数量=总价➗单价，所以列式是7.98➗4.2

师：大家同意吗？

生齐：同——意——！

师：观察一下，这个小数除法与前面的小数除法有什么不同？

生6:这题是：除数是小数的除法！

（师板书课题，启发）是啊！前面我们学了除数是整数的小数除法，这里除数是小数的除法。怎么办？有没有好办法？

（学生思考片刻，一双双小手举起来了）

生6:把除数是小数的除法转化成除数是整数的除法，把4.2变成42;

师：这是个好办法，把4.2变成42。被除数呢？（学生回答也移动小数点位置后）现在有转化后的三个竖式，你们认为选择哪一个才是正确的呢？理由是什么？（大屏幕出示）

算式1: 4.2）7.28 算式2:  4.2）7.28   算式3: 4.2）7.2.8

（学生齐声：选择3）

生7:根据“商不变的规律”把被除数和除数是同时乘10，否则商就会变。

生8:算式1: 4.2×10是42，被除数还是7.98，商就缩小了10倍。算式2: 4.2变成42，乘了10；7.98变成798，乘了100，商扩大了10倍。

生9:我补充：同时乘10，只要划去原来的小数点，同时，把小数点向右移动一位。

生10:我上黑板用箭头表示，就一目了然了。（边说边在黑板上表示出转化过程）

4.2．）7.2.8

 

师：同意吗？

齐：同——意——！

师小结：同学们真棒！运用商不变的规律，把除数是小数的除法，转化成了已学过的除数是整数的除法，会竖式计算吗？试一试！

……

【评析：】

除数是小数的除法，是典型的利用旧知“除数是整数的小数除法”作为新知生长点的案例。这里，教者在课始，直接出示了一组填空：①1250÷250=（     ）÷25，这是过去学过的知识，以唤起对知识的回忆；②8÷0.5=（    ）÷（0.5×2），这虽然是新知，但设计时，指定了0.5×2，运用旧知也可以解决，有意无意地孕伏了新旧知识间的迁移；③0.48÷2.4=（     ）÷24这题是例题类型，又帮学生架了个“桥”，引导学生思维“爬坡”——把除数2.4直接写成24（指定了乘10）；④1.6÷0.04=（    ）÷4，这题把转化成被除数添0这个难点直接暴露在学生面前，让学生在旧知不断支撑的前提下，突破了“除数是小数的除法”的难点和重点，由此，引出例题三个竖式正确的选择，成了水到渠成。所以，引导旧知回顾，支撑新知生长，在此反应得淋漓尽致。

 

二、引发新知总结 点拨旧知延续

    一个新的知识点学习后，往往对新知进行总结。常用的方法是：这节课我们学习研究了什么？你有什么收获可以与大家分享？还有什么问题……

其实，这是站在本课知识点的角度去总结的。殊不知，还有更高层次的总结，即把本课知识纳入学生已有的知识结构，作为旧知的延续，更利于学生重新建构。

   实录二：求一个数的几分之几是多少（片段）

……

师：同学们，通过刚才的学习，你有什么收获可供同学们分享？

生1:求一个数的几分之几是多少，用乘法计算。

生2:先找出单位“1”的量，把单位“1”的量×比较量对应的几分之几=比较量。

师：你们还有什么疑惑或什么问题想提出来的吗？（见没反应）你们没有问题，我倒有一个疑问，大家愿意一起讨论吗？

齐：愿——意——！

师：我感觉求一个数的几分之几的问题，有点类似以前学过的求一个数的几倍是多少？它们之间是否有联系？有哪些联系？大家可以讨论一下！

（一石激起千层浪，话音刚落，就讨论开了，讨论了若干分钟，反馈）

生3:我感觉单位“1”的量，相当于低年级的每份数或者一份数。

生4:我补充：也相当于中年级的1倍数或1倍量。

师：也就是它们的相同点是：单位“1”相当于1份数、1倍量，同意吗？

生齐：同意！

师：这个几分之几呢？与倍数之间有什么关系？

生5:这个几分之几相当于份数或倍数。

生6:我也这么认为，不过这里不满1倍，用几分之几表示。

生7:每份数×份数=总数；1倍数×倍数=几倍数；单位“1”的量×比较量的几分之几=比较量。

前面两个数量关系的份数或倍数都大于1，后面不满1，所以用几分之几表示？

师：大家感觉刚才几位同学说得有道理吗？

生齐：有道理。

师：是的！其实三个数量关系式可以用一个乘法关系去理解：当份数是大于1的自然数时，表现为前两种形式；当大于1的小数时，表现为第二种形式；当不满1时，就用分数几分之几表示，即求单位“1”的几分之几（倍）是多少。不过因为不满1倍，通常不说“倍”而已。

生8:那我们以后解答这类问题，就当成倍数问题去思考就行了！

生9:从此，这个内容再不陌生了，不过是倍数问题换了一个马甲！

……

【评析：】

许多学生往往把分数问题割裂开来学，给认知造成困惑，本课中教者有意抛出了一个疑问，让学生展开讨论，教者再适时点拨，让学生在讨论中，把新知当作旧知的延续，使认知不断完善，使认知不断完善，建构不断充实，起到了积极的作用，体现了教师的主导作用，同时也体现了学生的主体作用。

三、引领知识整理 启迪主动建构

    学生学了一系列知识后，我们有必要让它们进行整理与复习，启迪对知识进行主动建构。在单元复习和总复习中常见。这样把知识点连点成线，连线成面，有利于学生牢固掌握知识结构。

    案例实录：“多边形的面积”整理与复习（片段）

师：观察这两个梯形，你有什么发现？（如图）

 

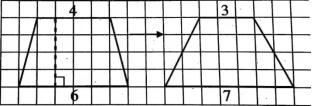
生1:它们的高相等，面积也相等。

师：请关注一下梯形的上底和下底。

生2:它们的上、下底的和都是10，相等。

师：如果梯形的高相等，面积也相等，梯形的上底和下底的和——

生：（齐）一定相等。

师：是不是一定相等呢？

生3:因为梯形的面积=（上底+下底）×高÷2，上、下底的和及高分别是算式中的两个因数，因数相同，积一定相等。所以反过来，积与其中的一个因数不变，另一个因数一定不变，也就是上、下底的和相等。

师：说得真棒！想象一下，还有和它们高相等、面积相等的梯形吗？

生4:上底是2，下底是8。

生5:上底是1，下底是9。

师：凭你的直觉，如果让它继续变下去，可能会变成什么情况呢？

生6:三角形。

生：这是上底是0，下底是10，上、下底的和还是10。

师：看来，梯形和三角形之间有一定的联系，三角形可以看作上底是0的特殊梯形。刚才是上底逐渐缩短，下底逐渐扩大，如果上底扩大、下底缩短，上、下底的和仍然等于10，面积会怎么样呢？形状又会怎么样呢？你发现了什么？

生7:面积不变，形状变成了平行四边形或者长方形。。。。。。

生8:平行四边形和长方形可以看成上、下底相等的特殊梯形。

生9:我发现：用梯形的面积公式竟然可以计算长方形、正方形、三角形、平行四边形的面积。

……

【评析：】

从观察梯形开始，让学生感受到：只要保证上、下底的和与已知梯形上下底和相等，即和是10的条件下，对上底缩短，下底扩长，进行“量变”，到上底为0，下底为10的“质变”。这个过程，构通了三角形与梯形的联系；反之，又通过上底扩大，下底缩短，直至上、下底相等，又一次从量变到质变，变成长方形或平行四边形。这样，梯形面积计算公式成为了长、正方形、平行四边形、三角形面积计算的通用方式，成了“百搭”与课始的公式推导，形成反差。沟通了多边形之间的关系，加深了的多边形的认识。

    “正是主体已有的认知结构为新的认识活动提供了必要的认识框架，而新的认识活动又往往会导致认知结构的分化、扩展和重组”。郑毓信教授这句话来概括，最恰当不过了。