巧建运动模型   速解往复运动

潘华君  任才生

（江苏省宜兴第一中学  江苏 无锡  214200）

摘要：往复运动是高中物理中常见的一类多过程运动，由于运动的复杂性以及与其它知识的结合考查，从而使这类问题成为较难题，要求学生具有较强的分析、综合能力．本文拟从一个简单习题入手，分析往复运动的特点，建立运动模型，以加深学生对这类问题的认识，提高学生分析问题和解决问题的能力．

关键词：运动模型  往复运动  应用  外推

物理模型的建立过程是一个抽象思维和形象思维相结合的过程，在高三的复习教学过程中，有意识地引导学生运用模型处理问题，并帮助学生总结、归纳，不但可使学生加深对物理概念、规律的理解，提高解题技巧，而且对发展学生的迁移思维和创造性思维起着很大的作用．本文也从这一角度出发，以高中阶段常见的往复运动为例，建立模型，合理外推，提高学生分析问题和解决问题的能力．

一、运动模型：

例1  一质量为m的小球原来离地高度为H，现将其从静止开始释放，运动过程中所受阻力大小恒为f（f<mg），小球与地面碰撞前后的动能不变，试分析小球最终停在何处和全程的总路程．

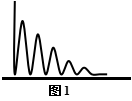解析  关于小球最终的位置可从三个角度分析：（1）从力角度看，由于f<mg，则小球最终只能停在地面上；（2）从运动角度看，小球做往复运动，但上升阶段减速运动的加速度大于下升阶段加速运动的加速度，即对每一次往复运动而言，后半段上升的最大距离必比前半段下降距离小，轨迹如图1（注：小球实际运动为竖直方向上的往复运动，但为体现它的往复性，作轨迹图时有意在水平方向上错开），终态必是停在地面上；（3）从功能关系角度看，在多次往复运动过程中，空气阻力不断做负功，小球的机械能一直在减少，小球不断的向地面处趋近．

设全程总路程为S，由动能定理得：

，

解得．

点评  本题描述的是一个往复运动的模型，处理时应着重分析三点：（1）选取合适对象，结合受力分析运动过程；（2）由于往复运动中，研究对象往往要受到阻尼的影响，最终要趋向某一定态，故必须分析收尾状态；（3）选取恰当的初、末状态，全程处理． 

二、模型等效

例2  质量为m的滑块与倾角为θ的斜面间的动摩擦因数为μ，μ<tanθ，斜面底端有一个和斜面垂直放置的弹性挡板,滑块滑到底端与它碰撞时没有机械能损失，如图2所示．若滑块从斜面上高为h处以速度v₀开始沿斜面下滑，设斜面足够长，求：(1)滑块最终停在何处?(2)滑块在斜面上滑行的总路程是多少? 

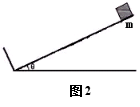解析  （1）从力角度看，由于μ<tanθ，即滑块所受摩擦力小于重力沿斜面向下的分力，则最终滑块只能停止在挡板处；

（2）对全过程由动能定理得：

，

解得：．

点评  本题是往复运动模型在斜面上的直接运用，依据模型特点，从合适的角度切入，迅速判断终态位置，选用恰当规律求解，问题必可迎刃而解．

例3  如图所示，AB和CD是半径为R=1m的1／4圆弧形光滑轨道，BC为一段长2m的水平轨道．质量为2kg的物体从轨道A端由静止释放，若物体与水平轨道BC间的动摩擦因数为0.1．求：(1)物体第1次沿CD弧形轨道可上升的最大高度；(2)物体最终停下来的位置与B点的距离．

解析  （1）设第1次沿CD弧形轨道上升的最大高度为h，由动能定理得： 

解得：h=0.8m．

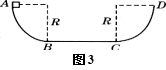（2）物体在圆轨道和水平面上做往复运动，最终必停于水平面上，设在水平面上滑行的总路程为S，则对全程由动能定理得：

，

解得：S=10m．

则物体最终停在C点，距离B点为2m．

点评  本题所涉及的运动是由圆周运动和直线运动“串联”而成的多过程运动，其模型可等效为上文所提的往复运动模型，着重考查了学生能否在新的情景下，利用等效的思想迅速建模、处理问题的能力．

三、模型外推

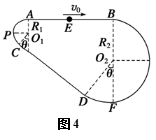例4  如图４是放置在竖直平面内游戏滑轨的模拟装置，滑轨由四部分粗细均匀的金属杆组成:水平直轨AB，半径分别为R₁=1.0 m和R₂=3.0 m的弧形轨道，倾斜直轨CD长为L=6 m，AB、CD与两圆形轨道相切，其中倾斜直轨CD部分表面粗糙，动摩擦因数为，其余各部分表面光滑．一质量为m=2 kg的滑环（套在滑轨上），从AB的中点E处以v_o=10 m/s的初速度水平向右运动．已知θ=37°（g取10 m/s²）求：（1）滑环通过O₁最高点A的次数；（2）滑环克服摩擦力做功所通过的总路程．

解析　（1）在A点处，滑环的临界速度为0，即只要，滑环就能过A点．设小球刚好能通过A点N次，对全程由动能定理得：

，

解得：N=6.25，即小环能通过A点6次．

（2）在小环通过A点6次后，由于，小环不可能停在CD直轨上，只能在滑轨的下半部分做往复运动，由于CD部分摩擦的作用，小环上滑的最大距离逐渐变小，不断趋向于D点，故小环的终态是在DD^/两对称点间的圆轨道上来回滑动．以E点为初态，D点为终态，对全程由动能定理得：

，

解得：m．

点评  本题以生活中常见的游戏滑轨为背景，以往复运动为载体，考查多方面知识点，综合性较强，需要学生具有很好的分析、综合能力．同时，从上面分析可知，本题所涉及的往复运动的终态不再是静止状态，而是一个无阻尼的往复运动．这是本文例1所提模型的延伸，考查学生的迁移能力．解决本题时需特别注意末状态的选择．从理论上讲，该问中末态可选在DD