交流发电机模型的构建和应用

——从2012年一道高考题谈起

2012年高考江苏卷第13题（即计算题第1题）将交流发电机模型和辐向磁场模型糅合在一起，着重考查了学生在新情景下的建模能力和迁移能力。但从多种渠道了解的信息看，学生失分情况较严重，主要原因是不能将习题与原有的发电机模型进行类比、外推，构建正确、恰当的新模型。本文拟从一道简单习题出发，从不同角度入手，构建两类模型，合理外推，以加深学生对这类问题的认识，提高学生分析问题和解决问题的能力，同时也为以后的高三习题教学提供参考。

一、构建模型：

例1    一正方形线圈，边长为L，匝数为N，在场强为B的匀强磁场中绕中心轴做匀速转动，如图1，角速度为ω，磁场方向与转轴垂直．当线圈转到平行面位置开始计时，

写出线圈中感应电动势随时间变化的表达式？

 

 

解析    解法一    构建切割模型

线框在匀强磁场中匀速转动时，起到切割作用的是ab和cd两边，作俯视图，如图2．从平行面开始计时，设线框经t时间转过θ，对一条ab边有

且

对cd边也具有相同规律，则框产生的总电动势为

解法二    构建磁通量变化模型

从平行面开始计时，设线框转动t时间，则

由法拉第电磁感应定律知

当然，若线圈从中性面开始计时，方法类同，此处不再复述。

点评    对于本题，采用了两种解法，解法一的目的是建立一个清晰的切割模型，从中可发现，正是有效切割速度在发生正余弦变化才产生了正余弦交流电，这是该交流发电机模型的实质．解法二是考虑到现行高中数学教材中已涉及简单的微积分，可以从磁通量变化角度入手，运用数学公式求解，其目的是为了与感生电动势建立类比，学生更容易接受．同时也可以证明，不论转轴在何处，只要转轴与磁场垂直，上面结论均成立．“线框在匀强磁场中匀速转动切割”是交流发电机的基本模型，对其的深入理解有助于分析各类变式题．

二、模型等效

1.有效切割速度正余弦变化

例2    如图3所示，ab、cd为两根水平放置且相互平行的金属轨道，相距L，左右两端各连接一个阻值均为R的定值电阻，轨道中央有一根质量为m的导体棒MN垂直放在两轨道上，与两轨道接触良好，棒及轨道的电阻不计，摩擦不计．整个装置处于垂直纸面向里的匀强磁场中，磁感应强度大小为B．棒MN在外驱动力作用下做简谐运动，其振动周期为T，通过中心位置时的速度为v₀，则此电路的电功率为：
    A．    B． C．  D．

解析    导体棒在外力作用下做简谐运动切割磁感线，产生的是正余弦交流电，若按正弦交流电处理，则，此电路的总功率为，故选B．

点评    本题与例1切割模型类似，用“杆的平动”替代“框的转动”，但均是利用有效切割速度的正余弦变化来实现交流电的产生，是例1的直接应用，依据模型特点，从合适的角度切入，选用恰当规律求解，问题必可迎刃而解．

2.有效切割长度正余弦变化

例3    如图4所示，两根不计电阻的倾斜平行导轨与水平面的夹角θ=37^o ，底端接电阻R=1.5Ω.金属棒ab的质量为m=0.2kg.电阻r=0.5Ω，垂直搁在导轨上从x=0处由静止开始下滑，金属棒ab与导轨间的动摩擦因数为μ=0.25，虚线为一曲线方程y=0.8sin(x)m与x轴所围空间区域存在着匀强磁场，磁感应强度B=0.5T，方向垂直于导轨平面向上（取g=10m/s²，sin37^o=0.6，cos37^o=0.8）． 求：若金属棒以2m/s的速度从x=0处匀速下滑至X_o=6 m处，电阻R上产生的焦耳热为多大？

解析    本题所描述的情景是一金属棒匀速切割的问题，但在过程中，其有效切割长度是按正余弦变化的，所以产生的也是一个正余弦交流电。由于题中没有直接给出外力的情况，若仍从功能关系或能量守恒角度求解会很复杂。因此，本题仍利用焦耳热公式求解。设a b棒运动至x处，则由曲线方程知

m

   此时产生的感应电动势为

，其中

则棒从x=0处下滑至X_o=6 m处，R上产生的焦耳热为

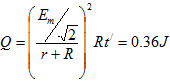
点评   本题将匀强磁场约束在一个由一段正弦曲线所围的区域里，从而实现有效切割长度的变化，突出考查了从实际问题中抽象概括、构建物理模型的创新能力．从上面分析也可以看出，本题与例1的切割模型是可以代换的，是“用长度的正余弦变化”替代了“切割速度的正余弦变化”．

3.磁感应强度在空间上正余弦变化

例4    足够长且电阻不计的金属光滑导轨MN、PQ水平放置，导轨间距为d，M、P两点间接有阻值为R的电阻，建立平面直角坐标系，坐标轴x，y分别与PQ、PM重合，如图5所示．空间存在垂直导轨平面且范围足够大的磁场，磁场沿x轴的分布规律为，其中B₀ 、λ为常数，以竖直向下方向为B 的正方向．一根电阻不计的导体棒AB垂直导轨放置，在与棒垂直的水平外力F的作用下从非常靠近y轴的位置以速度v匀速向x轴的正方向运动，运动过程中，棒始终与导轨垂直．求： (1)导体棒运动到哪些位置，回路中的电流达到最大值；(2)在发生一个λ位移的过程中，电阻R上产生的焦耳热．

解析    （1）导体棒在向右运动过程中，某时刻有

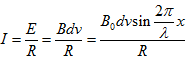
由该式可知，电流最大处应是正弦函数取最大值时，则

（2）由上问可知电流随空间位移是正余弦变化的，又因为导体棒在匀速运动，则电流随时间的变化规律为

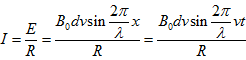
即产生的是一正弦电流，在一个λ位移内，交流电刚好变化一个周期，则

点评    磁场随空间位置变化——这是两类典型变化磁场之一，此处需明确的是没有感生电动势只有动生电动势，这也是学生易出错的地方．本题所涉及的模型与例1相比，仅是将“有效磁场的正余弦变化”替代了“有效切割速度的正余弦变化”，两者模型也是可以代换的．

4.磁感应强度随时间正余弦变化

例5    如图6所示,两根足够长的平行导轨处在与水平方向成θ角的斜面上, θ=37⁰,导轨电阻不计,间距L=0.3m.在斜面上加有磁感应强度B=1T、方向垂直于导轨平面向上的匀强磁场．导轨底端接一个阻值R=1Ω的电阻．质量m=1kg、电阻r=2Ω的金属棒横跨在平行导轨间．已知h₁=2.0m，sin37°=0.6，cos37°=0.8，g=10m/s² .求：若将ab棒固定在导轨上，磁场按图7所示规律变化(2.5×10^-2∽7.5×10^-2s内是正弦规律变化)，电阻R在一个周期内产生的焦耳热为Q=5J,取,求B₀．

解析    由题意可知，在0∽T/4内，磁场均匀变化，即电动势应是一定值，则

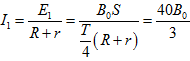
在3T/4∽T内,磁通量的变化率与0∽T/4内数值是一样的，则

在T/4∽3T/4内,磁通量的变化规律为

由法拉第电磁感应定律知

则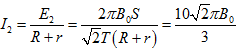

一个周期内产生的焦耳热

代入数据可得B₀=0.5T

点评   当磁场随时间变化时，回路中要产生感生电动势。上例中T/4∽3T/4内磁通量的变化规律与本文例1解法二所构建的模型是等效的，着重考查了学生能否在新的情景下，利用等效的思想迅速建模、处理问题的能力．

三、模型外推

例6    （2012年高考江苏卷第13题）某兴趣小组设计了一种发电装置,如图8所示.在磁极和圆柱状铁芯之间形成的两磁场区域的圆心角α均为,磁场均沿半径方向.匝数为N的矩形线圈abcd的边长ab=cd=L、bc=ad=2L. 线圈以角速度ω绕中心轴匀速转动,bc和ad边同时进入磁场. 在磁场中,两条边所经过处的磁感应强度大小均为B、方向始终与两边的运动方向垂直. 线圈的总电阻为r,外接电阻为R.求:(1)线圈切割磁感线时,感应电动势的大小Em；(2)线圈切割磁感线时,bc边所受安培力的大小F；(3)外接电阻上电流的有效值I.

解析    （1）由题意可知，线框在转动中仅bc、ad 两边切割，其运动速度

转动中,始终有B⊥v,类比例1解法一所建立的切割模型可知，本题中的有效切割速度始终为v,则感应电动势为

（2）对bc边有

（3）一个周期内，通电时间为

对外电阻R，由有效值定义知

解得

点评    试题将交流发电机模型和辐向磁场模型糅合在一起．辐向磁场在整个高中物理教材中着墨不多，命题者将其作为一种信息给出，需要学生提炼，从而形成清晰的切割情景．同时，从上面分析可知，本题中的有效切割速度不再是正余弦变化，而是始终不变，这是本文例1所提模型的延伸，考查学生的迁移能力和类比建模能力．

四、结束语

物理模型的建立过程是一个抽象思维和形象思维相结合的过程，在高三的复习教学过程中，有意识地引导学生运用模型处理问题，并帮助学生总结、归纳，不但可使学生加深对物理概念、规律的理解，提高解题技巧，而且对发展学生的迁移思维和创造性思维起着很大的作用．从上面例题分析可看出例1起到了一个很好的解题模型的示范作用，其它几题均是它的变式和延伸．在物理学习中，将一类问题糅合到一个典型问题中从而建立一个模型，对提高学生分析、解决问题的能力很有帮助．