圆锥的体积

一．教学目标

1.使学生利用已有知识自主探索并掌握圆锥的体积公式，能应用公式正确计算圆锥的体积，并解决相关的简单实际问题。

2. 使学生通过操作、观察、猜想、交流和归纳等数学活动，经历圆锥体积公式的探索过程，体会用实验研究问题、获得结论的方法，积累立体图形的学习经验，培养抽象、概括和推理能力，发展空间观念。

3，使学生体会数学知识内部之间的联系，感受数学知识的奇妙和内在魅力，激发学习数学的兴趣和积极性。

二．教学重点和难点

教学重点：圆锥的体积计算。

教学难点：圆锥的体积公式推导

三．教学准备

等底等高的空心圆柱和圆锥各一个，沙子，多媒体课件。

四．教学过程

（一）复习导入

1. 回顾旧知。

教师出示一个圆柱形物体。

提问：圆柱的体积是怎样计算的？（板书：圆柱体积=底面积×高）想想，我们是如何推导出圆柱体积公式的？

再出示一个圆锥形物体，指名说说圆锥的特征及各部分名称。

2.揭示课题。

提问：我们已经认识了圆锥，知道了它的特征。你还想学习圆锥的哪内容？

引入：许多同学想到了圆锥的表面积和体积。关于圆锥的体积，应如何计算呢？这节课我们就来研究个问题。

（板书课题：圆锥的体积）

（二）自主探究

1. 提出猜想。

谈话：老师准备了一个空心圆柱和圆锥，仔细观察、比较小组里的圆柱和圆锥，各部分之间有怎样的联系？

学生交流，得出结论：每小组的圆柱和圆锥底面积相等，高也相等，我们可以简称它们“等底等高”。（板书：等底等高）

提问：你能估计出圆锥的体积是圆柱的儿分之几吗？（指名学生估计）

2.实验操作。

提问：圆锥的体积到底是与它等底等高的圆柱体积的几分之几呢？有什么办法来验证估计的结果呢？

学生交流自己的想法。

引导：按照大家交流的想法，我们可以用实验来得到答案。

出示实验要求：小组合作，在圆锥容器里装满黄沙，然后倒入圆柱容器里，看看倒几次正好装满，完成后各小组交流实验结果。

学生上台实验操作。

3. 得出结论。

提问：通过实验你发现了什么？（各小组交流结果）

得出：从倒的次数看出，圆锥的体积是与它等底等高的圆柱体积的，或者说成圆柱体积是与它等底等高圆锥体积的3倍。

追问：是不是所有的圆柱和圆锥都有这样的关系呢？我们来看其他容器。

教师出示底和高不全相等的圆柱和圆锥，演示操作实验过程。

提问：这个圆锥的体积也是这个圆柱体积的，吗？为什么？

强调：圆柱与圆锥只有在等底等高时，圆锥体积才是圆柱体积的，圆柱体积才是圆锥体积的3倍。

【设计说明：通过实验操作，学生已经有了等底等高的圆锥与圆柱的直观感知。为了突出“等底等高”的特点，进一步安排了对比实验切实理解和认识圆锥体积是和它等底等高圆柱体积的。强调“等底等高”这个前提条件，有利于学生准确推导圆锥体积计算公式，并培养学语言表述的严谨性和思维的严密性。】

4.推导公式

提问：通过刚才的实验结果，想一想，可以怎样求圆锥的体积？你怎么想的

根据学生交流，教师板书：

圆锥体积=等底等高的圆柱的体积×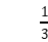

                =底面积×高×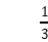

引导：如果用V表示圆锥的体积，S表示圆锥的底面积，h表示圆锥的高，圆锥体积的计算公式可以怎样表示？

学生回答，教师板书V=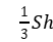

提问：求圆锥体积需要知道哪些条件？公式中的底面积乘高表示谁的体积？为什么要乘？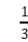

5. 回顾反思。

提问：回顾圆锥体积公式的探索过程，你有什么体会？

引导交流并小结：探究圆锥体积的计算，我们是联系已经学过的圆柱的体积计算，从圆柱体积公式想起，通过比较等底等高的圆锥和圆柱的体积，想到可以用实验方法探索圆锥的体积公式。通过实验验证，发现了等底等高的圆柱和圆锥的体积关系，得到了圆锥体积的计算公式。由此可以看出，学习数学，可以联系相关内容进行思考，并且实验也是探究、解决数学间题的重要方法。

6. 教学“试一试”。

学生自由读题后独立解答。

集体交流，让学生说出思考的过程。

提问：圆锥的体积应怎样计算？在计算时要注意什么？

三、巩固练习

1.做“练一练”第1题。

指名读题，学生独立完成。

提问：这题告诉了我们什么，要求什么？你是怎样计算的？（板书算式）为什么这样计算？

引导：如果圆锥的体积是9.42立方厘米，那么圆柱的体积是多少？请你列式计算。

集体交流，让学生说说是怎样想的。

说明：通过学习我们已经知道，圆锥的体积是与它等底等高圆柱体积的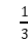,圆柱的体积是与它等底等高圆锥体积的3倍。