——以《分数的意义》教学为例

单敏

【摘要】

    数学学科具有自身固定的知识结构和学科探究过程，这个学科特点决定了教师要对教学内容进行结构化的组织，让学生将能像数学家一样经历知识的发生、发现过程，实现对知识的深刻理解，积累数学学习经验，发展数学思考。本文以苏教版五年级下册《分数的意义》一课的教学实践为例，探索了在概念教学中结构化教学的实践方式，总结了概念的结构化教学经验。

【关键字】

    结构化、结构化教学、数学素养

当前的数学教学中存在教师过度依赖教材编排，导致知识碎片化，缺乏对知识链的整体把握等问题。数学学科特点决定了数学知识中的一般概念、原理的教学将具有结构化的特点。布鲁纳指出：“不论我们教什么学科，务必使学生理解该学科的基本结构”。 ¹当对教学内容进行结构化组织的时候，学生将能像数学家一样经历知识的发生、发现过程，实现对知识的深刻理解。

结构是指不同的类别或者相同类别的个体或部分，按照相互之间的关系有序地组合而成的整体。数学知识的结构不仅包含数学的知识点，而且包含了知识之间的联系方式、逻辑线索以及数学思想方法。

结构化教学是从数学知识体系的结构化的特点以及学生身心发展规律出发，对学习内容的结构进行适当的重组和提炼，从而形成一种有高度、有层次感的整体认识，通过凝练知识核心，孕伏渗透知识脉络、反思回顾学习过程等方法，使上述结构内化为学生的认知结构。这将促进学生对知识的深刻理解，发展数学素养，实现数学学科独特的育人价值。

数学概念是数学思维的基本单位，概念的形成帮助学习者理解事物的从属关系，在新情境中同化与固着新的知识，因此具有很强的系统性。²教师在进行概念教学时应当采用结构化的教学方式，可以避免知识零散化现象，帮助学生在高点认识本体知识，全局性把握知识结构，感受整体性思维方式，发展数学素养。

苏教版五年级下册《分数的意义》一课是在分数认识领域的一节种子课。分数的定义一般认为有四种：份数定义、商定义、比定义和公理化定义。本课时要让学生理解份数定义，即把单位“1”平均分成若干份，表示这样的一份或几份的数叫做分数。这个定义可以理解为认识其他定义的起点。要理解分数的份数意义，首先需要理解单位“1”的含义；紧接着，需要有形象化的例子作为材料支撑，从丰富例子中提炼分数的共同本质属性。笔者通过对本课结构化的设计，帮助学生完整建构分数的意义，提升认知的结构化水平，发展数学抽象思维能力。

一、横向结构化,经历聚类归纳过程。

笔者以对单位“1”的认识为突破口，通过对单位“1”的多元表征，理解“单位”对于数的意义；接着通过对一个分数的多元表征，理解单个抽象的分数；然后通过对多个分数的意义归纳，提炼本课分数的意义。

1、 在多元表征中认识单位“1”。

教师首先依次出示单个物体、图形、计量单位、以及多个物体组成的整体，帮助学生建立“1”的概念，然后揭示：在数学上，1有时也被称为单位“1”。

接着依次出现如下物体，并用单位“1”来度量，让学生用不同的数表示度量的结果（如图1）。多次度量之后，单位“1”的概念支点被强化，学生能站在高位理解“单位‘1’”， 理解当度量不能出现整数结果时用分数表示，从整数到分数的认知屏障被突破。全新的分数与比较牢固的整数的认知结构建立联系，同时丰富了学生对一个分数的认识的表象，丰富而相似的原型给了学生充分的思辨、讨论的机会，利于学生对外部特征进行概括，抽象出单个分数的形式化定义。

（图1）

2、在多元表征中抽象单个分数的意义。

图1中，对单位“1”进行多元表征的同时，也对3/4这个分数进行了多元表征，利于学生理解其抽象意义——把单位“1”平均分成4份，表示这样3份的数。接着出示下图多个实例，让学生用分数表示涂色部分（如图2），并说说为什么不同的涂色部分，能表示同一个分数。最后引导学生脱离直观图说说7/11和99/100这两个分数的含义，以此及时巩固对分数意义的模式化表达。

（图2）

3、多次表征中提炼分数的意义。

在学生进行了多个分数的意义提炼的基础上，教师进一步呈现多个分数的意义的表达句式，提问：这些分数的含义有什么相同之处？你能概括地说说什么样的数叫做分数吗？引导学生从多个分数的意义中及时进行抽象概括出分数的意义——把单位“1”平均分成若干份，表示这样一份或几份的数叫做分数。

以上三个层次中，教师均以横向多元表征的方式，帮助学生积累丰富表象，学生在多层表征中能经历分数概念的形成过程，从对概念的外延丰富性的认识，走向抽象意义的深刻理解，认识水平从直观操作向分析水平提升。通过教学环节的结构化，学生思维的结构化水平得到发展。

二、纵向结构化——实现知识层级跃迁

学生形式化地掌握概念符号，而不理解本质含义的情况是经常发生的，所以教师应当把新概念的关键属性应用到更大范围的例子中，通过知识的前后对比、应用、拓展帮助学生对概念的掌握从外在直观动作表征向内部的深层表征提升，从而完善认知结构。

1、在对比中丰富概念认知

在揭示了分数的意义以后，笔者让学生把3个桃、6个桃、12个桃组成的整体分别分一分，涂色表示2/3。然后追问，为什么桃的个数不同，却都能表示出三分之二？为什么同样表示三分之二，桃的个数却不一样？学生又从抽象的分数回到具象的数量，就在这一个来回之间，学生体会到分数的无量纲性，对分数概念的认识更丰满。

当经历了上面这次的抽象意义和具体数量的来回跨越之后，教师出示：“五（1）班学生中，会打乒乓球的占5/9；地球表面2/3被海洋覆盖”等句子，让学生说说这几个分数的含义。引导学生继续从抽象的分数走向半抽象的情境，固化对分数概念的认识。

3、 在延伸中拓展知识结构。

布鲁纳说，掌握事物的结构，就是允许别的东西与它有意义地联系起来。学生掌握一个概念，还需要理解其与其他概念之间的关系。本课作为分数认识的起始课，对于后续认识如假分数、等价分数、分数的商定义等意义重大。笔者尝试依托数轴为学生未来学习分数的其他知识埋下伏笔（如图5）

    第一步：认识数轴上的1和“单位1”，接着让学生用分数表示三等分点的数；第二步：教师再把“1”平均分成6份，让学生表示各个点上的数；第三步：引导学生发现，有一些点能用两个分数表示，这在整数系统中是不曾出现的，以此渗透等价分数知识；教师随即提问，2/6和1/3是相等的，那么2/6比哪个分数大，比哪个小呢，引导学生理解分数有大小，可以进行比较；第四步：让学生以1/6为分数单位，依次数一数，最后出现了6/6，教师提问，有没有这样的分数？学生立刻异口同声地说，“没有”，但是瞬间又有学生开始嘀咕，“好像有……”，学生的这种愤悱的状态为后续的学习种下思考的种子。

在以上纵向结构化教学过程中，学生已有的现实经验和认识基础为理解抽象的分数意义提供了条件，教师帮助学生在具体情境和抽象形式之间反复跨越，建立联系，实现认知结构的纵向建构；通过在数轴上的分数的认识，孕伏新的知识点，使本课的学习具有了种子课的意义。

三、综合结构化——在纵横之间深化概念

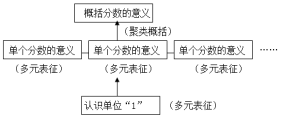
本课中，从单位“1”的建构，到单个分数意义的抽象，到分数意义的概括，再到分数在具体情境中的意义，“纵”与“横”的结构彼此咬合，呈现在学生面前的是一幅有层次，有内容，有延伸的分数意义发生、发展结构图。通过本课知识的学习，学生积累了类比推理、抽象提炼等多方面的学习经验，感悟到数学知识之间的紧密联系，这些学习经历将是学生进一步进行数学探索的宝贵财富。

认知发展理论告诉我们，概念的教学，要适合学生的认知发展水平和已有认知结构。概念和概念之间又是彼此联系的结构性关系。所以概念的结构化教学，教师不仅要重视新概念与学生生活之间的关系，也要重视概念之间的关系，重视正例和反例、变式的引入，帮助学生由表及里，由浅入深地完善概念结构。践行结构化的教学，能让学生“见树木，也见森林”，看到知识的发生发展过程，感悟知识之间的的隐性脉络，形成知识的意义结构；在掌握知识的同时，扩大数学视野，形成结构化思维，从会思考走向会学习。

参考文献

[1]张华.课程与教学论[M].上海教育出版社:上海,2018:18-19

[2]曹才翰 章建跃.数学教育心理学[M].北京师范大学出版社:北京,2000:88-95