【习题1】“小明的邮票是小红的4倍，两人各用了5张后，小明的邮票是小红 9倍，两人原来各有多少张？”

这是五年级某次数学应用能力竞赛中的题。五年级学生还没有学习过列方程解决问题。这一题的数量关系比较复杂，常规的列式计算的方法，学生可能难以理解。我平时有让学生在试卷上写出思考过程的要求，在翻阅学生试卷时，我发现多位学生采用了如下的方法：

我让学生说说自己的想法。

生1：我把小红和小明的数据列出来，然后分别减5，看看得数是不是小明的是小红的9倍。

师：那么列举的时候你为什么从6开始呢？

生2：因为小红和小明的数量应该比5多，用去5张才够。

这里使用了一一列举的策略，依次列举，逐步找到答案。这个方法没有体现出数学的抽象的特征和形式美，却实实在在解决了问题。这个看似笨拙的方法蕴含了朴素的数学思想。从学生的解题情况来看，这个方法应当是最接近学生最近发展区的方法。

为了让学生对一一列举的策略有更深入的认识，我接着追问：

师：这样的方法好在哪里？

生：思考起来比较简单，很好理解。

师：这样的列举和我们以前学习的列举策略有什么不同？

……

生：以前学习的列举策略能把所有答案列举完整，这里的列举不知道列完整了没有。

生：如果数很大，可能我们列举很久都找不到答案。

师：说得真好！

无独有偶，在最近一次练习中又遇到了一题：

【习题2】“一个梯形的下底长度是上底的3倍，高10厘米。如果下底减少12厘米，上底增加18厘米，就成为一个长方形。原来梯形的面积是多少平方厘米？”

本题中上底和下底之间的数量关系对大多数学生来说理解有难度。有一些同学采用了列举的方法找到了答案。

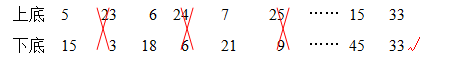
我在课堂上追问用以上方法的同学：

师：你是怎么想的？

生：这一题我觉得数不算大，就试一试用列举的方法，发现后来上底和下底越来越接近，最后就有了答案。

师：在遇到困难的时候你能很有耐心地列举，这是很好的做题态度……

为了让学生进一步探索上底和下底之间的关系，我继续采用线段图的方法让学生理解数量关系。（过程略）

师：用上面的列举方法和下面的画图列式方法都能解决问题，你觉得哪个方法你愿意用在以后的解决问题中？

生：第二个画图列式的方法！因为这个方法更通用。

师小结：看起来的确如此，但是每个方法都有自己的妙处。当我们不理解数量关系时，用一一列举的方法能找到答案或者找到解题的方法，用画图的方法也能帮助我们找到数量关系。我们以后要善于运用灵活使用各种方法解决问题。

【教后反思】

 以上两题都是非常规题。在学生以往的学习经验中，很少出现无法直接列式求解的问题。久而久之，学生的思维更趋向封闭，在长久的数学演绎的练习之后，遇到无法直接列式求解的问题，从纷杂的信息中找到关联，用相对开放的方法探索答案的思维方式就显得十分珍贵。本题中学生能突破常规，用自已有的经验解决问题，这样的解题思路本身值得赞赏。

在数学学习中，我们遇见的题不计其数，有些题做过了，下次遇见可能还是不能做对，但是解决数学问题过程中学习到的解题策略，积累的解决问题的经验会沉淀下来成为学生数学素养养成的基本元素，是学生认知结构中的“元认知”部分，成为学生未来发展的源动力。

数学教学在完成数学知识传承之外，更重要的是促进人的发展。我们理应站在发展的高度检视课堂教学，分析学习过程。我们应当努力让每一次的教学都成为学生发展向上的台阶——数学教学最终走向数学教育。