【摘要】课堂教学中的追问指的是教师针对前一个问题提出后学生的回答和反应再次发问，穷追不舍，追根究底，直到学生完全弄懂，弄通为止。是重要的师生活动方式。课堂追问在发展学生思维、促进学生主动建构方面有着不可忽视的作用，是重要的师生互动方式。本文从追问的价值、追问的实践策略、追问的现状评价几个方面阐述教师在课堂里如何认识追问价值，把握追问时机，促进学生认知的发展。

【关键词】追问  动态生成 认知发展

一、追问的价值探寻

教学行为是教师在课堂中影响学生的一切行为和表现，是为实现一定的目标或意图而实施的。课堂提问行为与课堂教学的历史同样悠久，是师生互动的课堂中最为重要的教学行为。通过提问，把教学的要求转化为学习的动机，使教学内容转化为学生的认知。

课堂教学中的追问是指教师在课堂中针对某一内容或问题，根据学生的回答或反应再次提问，穷追不舍，直到学生完全弄通弄懂。追问是在前次提问基础上的延伸和拓展，亦是提问行为，但又不同于一般的提问行为：提问是教师针对某一个知识点的教学，在课堂上逐个提出预设好的几个问题。而动态的课堂或者常有超出有教师预设的精彩，或者有教师意料之外的尴尬。所以追问是教师是对当时课堂出于预设之外时的主动介入的再问。教师通过课堂追问及时调整教学预设，抓住稍纵即逝的教学机遇，故课堂追问行为有不同于一般提问行为的心理功能，有其独有的课堂价值。     

积极有效的追问能让教师获取更多反馈信息，使课堂的调整有章可循；激发学生的再次思考，使学生之前的思考发挥作用，使思维连贯；突破教学的重难点，使数学知识本质得到凸显，学生认知趋向完善；传递教师情感，激起学生或惊奇，或喜悦的情绪，营造良好的课堂氛围，促进学生的积极学习。

二、追问的实践策略

每个一线教师每天都在课堂里进行追问，追问的积极功能的实现取决于追问的质量。针对学生的回答不假思索的发问，往往错失生成的时机，而恰到好处的追问则能提高学生思维的深刻性和完整性，促进学生认知的发展。

1、在思维缺席处追问。

如《解决问题的策略——画图》（四下）时有如下片段。

例题“梅山小学有一块长方形花圃，长8米，在修建校园时花圃的长增加了3米，这样花圃的面积就增加了48平方米。原来花圃的面积是多少平方米？”

有些同学已经在动手列式了，还有一些同学则面露难色。

师：解决这个问题有什么困难吗？

生：题目的意思我不太明白。

师：是不是每句话的意思都不明白？

生：是“花圃的长增加了3米，这样花圃的面积就增加了48平方米。”这句话不太明白。

师：只看文字的确比较难懂，有没有办法让大家明白这句话的意思？

生：可以画画图。

……

面对比较新颖的，陌生的问题，学生往往不知所措，这里的例题对于学生，是一个陌生的问题，因为对题意不理解，所以无从下手。此时教师如果提出“面对理解起来困难的题，我们可以用画图的方法来弄懂”，学生也能依着教师的设计画图理解。但是教师面对这样的状况不急于抛出“画图”这个策略，而是等待学生的反应。此时学生的回答“题目的意思我不太明白”，教师即顺势而为，一步步追问，帮助学生拨云见日，找到困难的核心，让学生经历寻找策略的过程，使“画图”的出现水到渠成。数学教学的重点不是解题技术，而应当是数学核心概念和思想方法。叶圣陶先生也认为：“教师之为教，不在全盘授予，而在相机诱导。——上善若水，因物赋形。”在学生遇到问题缺乏思维方法时，教师应当把握住机会，通过步步紧逼的追问，帮助学生从疑惑中找到出路。

 

2、在深度匮乏时追问。如《找规律》（四上）一课中：

师：我们生活中有没有这种间隔排列的规律呢？

生：课桌和椅子是间隔排列的。

师：那看这一排的课桌，是几张？我们数数。（6张）椅子是几张？

生：（齐答）不知道

师：不知道？数一数，能不能知道？

生：1、2、3……6张！

师：数一数可以知道6张椅子，那不数可不可以？

部分学生：不可以。

部分学生：可以。

师：不数，怎么知道？

生2：一张桌子和一张椅子一一对应，刚刚好，所以桌子和椅子是一样多的。

 

    当老师问到这一排的课桌是6张，椅子是几张时，有些学生因为不能看到所有的椅子，所以一时回答不出来，老师让学生数一数，部分学生看得到椅子，立刻数一数，知道了答案。显然数一数的方法是思维层次比较低的，老师也没有停留于学生发现这个间隔排列的现象。进一步追问：不数能不能知道？立刻激发起学生思考的热情，让学生用刚刚学到的知识解决间隔排列的问题，，使学生用数学的眼光看生活的同时，用数学的思维想生活。

老师的追问不能不顾学生实际,硬要学生达到他们不可能达到的高度，也应避免思维层次低的重复追问，应当以上老师这样根据学生已有的认识和能力提出合适的问题，使学跳一跳摘到桃子，从而有效开发学生的最近发展区, 让学生在老师的追问后能有所思所悟，提升学生的认知潜力,促进学生的发展。

3、在认识偏差时追问。

例如，在教学《点到直线的距离》这一课时

出示例题：

 

 

 

 

 

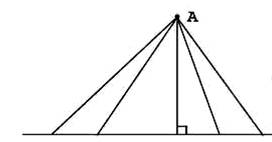
师：量一量从A点到已知直线的这几条线段的长度，你有什么发现？

生1：我发现画在中间的这条线段最短。

生2：我也发现如果从A点向这条直线画线段，中间的最短。

从图上看的确是中间的线段最短，图中的信息不足以让学生认识到最短线段和垂直线段的关系，故而产生了认识偏差。此时如果告诉学生中间的这条线段与已知直线是互相垂直的，所以在这些连线中垂直线段最短，显得牵强，学生并不能将此内化为自己的认识，不是最佳的解决办法。但是。于是教师在图上又画了两条线段（如下图），然后追问：

 

 

 

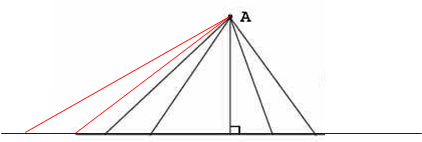
师：现在观察从A点向已知直线所画的这些线段的长度，你认为哪条最短？

学生开始议论纷纷，有些学生已经举手急于发表自己的意见了。

生3：我认为是那条垂直线段最短。（学生纷纷表示同意）

师：刚刚你们还说是中间的线段最短的，现在怎么又变成说“垂直线段最短了”？

生4：因为那一条是垂直的，原来只有5条线段，那条垂直的在中间，是中间的最短，现在多画两条了，就应该是垂直的线段最短了。

······

经过对第二个图的讨论，学生们已经撇开了问题的非本质信息，深入地认识到了“垂直线段最短”，理解了第一幅图中为什么是中间的线段最短。

学生因为认识水平的原因，往往对问题的认识停留在表面而沾沾自喜，面对这样的情况，老师要做的不是牵强地把学生的思维引入教师的预设，而应当适时引导，使学生在教师恰当的追问下跳出认识的误区。追问就像路标，让学生迷途知返，并且让学生由表及里地把握知识的本质，获得思维的快乐和认识的提升。

 

4、在本质探究处追问。

在上《长方形和正方形的面积计算》一课时：

教学完长方形的面积计算后，出示了一个长12厘米，宽5厘米的长方形让学生利用公式计算面积。然后把这个长方形长变短，成为一个长5厘米，宽5厘米的正方形，出现了下面一个片段。

师：现在变成了一个什么图形？（正方形）

师：这个正方形的面积应该怎么计算呢？

生1：5乘5等于25平方厘米。

生2、3：（激动地）老师，我有不同意见，应该是5乘4等于20平方厘米。

生4：我觉得是5乘5等于25。

师：那么哪些同学认为是25平方厘米？（只有4个同学没有举手。）

师：那么你们能说说为什么是25平方厘米吗？

生：这个正方形里摆小正方形，一行可以摆5个，可以摆5行，5乘5等于25平方厘米。

师：那谁能说说5乘4等于20算出了什么？

对于计算长方形和正方形的面积就是计算图形里面包含多少的面积单位这个知识本质，学生已经通过前面的教学有了初步的认识，但是以前只计算过正方形的周长，没有计算过正方形的面积，尽管正方形的出现有了自然的铺陈，但是依然出现5×4的算法，可见正方形的周长在学生的头脑中根深蒂固的影响。所以引导学生说出为什么要用5乘5来计算时，计算图形面积的本质再一次被凸现出来。认为用5乘4来计算面积的学生虽然只有少数，课上到这里似乎已经到位了，可是课堂的追问不是为了问出一个答案，而应当是启迪学生智慧的钥匙，老师不失时机地又一次追问“5乘4等于20算出了什么”，引导学生对问题进行换向思考，挖掘学生产生错误的原因，对比计算周长和计算面积的本质的不同，帮助学生从正反两个方面把握面积知识的本质。类似这样的追问在课堂中并不少见，教师应当在知识本质凸显处通过穷追不舍的追问使学生厘清知识内涵，认知得到发展。

5、在教学等待后追问。

如：教学中遇到这样一个判断题：

把一个1立方分米的盒子摆在桌上，所占桌面的面积是1平方分米。（   ）

在读完题的第一时间，全班整齐划一地认为这句话是对的。学生思维受到1立方分米正方体的局限，出现这种现象在学习体积之初实属正常。此时教师让学生把想法和同桌说一说，照理说学生的认识是一致的，交流也不会有不同的结果，但是一分钟后反馈学生的想法时事实恰好相反：

师：说说看你是怎么想的？

生：我明白了，这句话是不对的，因为这个盒子不一定是正方体的。

生2:1立方分米的盒子可能是个正方体，也可能······

当教师确认思维材料符合学生的思维能力时，如果学生没有达成预设的目标，教师要做的不是越俎代庖，而是给他们时间。如果教师急于自己上阵，在学生没有充分思考的情况下帮助学生思考，帮学生回答，会使学习陷入灌输式的境地。学生的思维活动有特定的节奏，有时顿悟，有时冥想，有时则需要时间来磨练。在师生互动的课堂里，教师的追问要贴合学生思维的节奏，太快学生跟不上，太慢拖拉又浪费课堂资源，造成学生思维游离，都不利于学生认知的发展。

 

目前对教学行为的研究中，大多数是对一般的提问行为的研究，对于课堂追问行为的单独研究比较少。事实上，课堂中的追问是具有普遍性的教师教学行为。苏霍姆林斯基说：“教育的技巧并不在于能预见课的所有细节。而在于根据当时的具体情况巧妙地在学生不知不觉中做出相应的变动。”可见进行有效的课堂追问需要教师具有比较高的课堂把控能力。

《课程标准》指出学生是学习的主体，教师是学生学习的参与者、合作者、引导者。在课堂里教师的主导作用是明显的，教师的教学行为引起、维持、促进着学生的活动，教师对学生的理解和教师个人的教育信念、教学理念和教育哲学是在课堂上的所有教学行为的目的根源。教师要树立“生为本”的教学观，放下“知识本位”，“教师权威”的观念，准确深入理解学生，尊重学生的思维发展规律；深刻解读教材，进行充分的课堂预设；不断总结课堂教学的经验，提高自身在课堂中把握动态的资源的能力，改善课堂追问行为。课堂追问要有明确的指向，切准问题核心，避免盲目的，不假思索的追问；也要避免重复的低层次的重复追问，要以学生数学认知发展为追求，用恰到好处的追问引领学生思维，凸显知识本质，在不着痕迹，游刃有余的追问间促进学生认知发展。

 

【参考文献】：

1. 申继亮, 李茵. 教师课堂提问行为的心理功能和评价[J]. 上海教育科研, 1998, (6): 40-43
2. 彭亮. 教师话语的有效性研究[D]. 南京:南京师范大学, 2013. 41-45
3. 叶立军. 数学教师课堂教学行为比较研究[D]. 南京:南京师范大学, 2011.