摘  要：“我们要活的书，不要死的书；要真的书，不要假的书；要动的书，不要静的书；要用的书，不要读的书。总起来说，我们要以生活为中心的教学做指导，不要以文字为中心的教科书。”陶老的“教育即生活，生活即教育”理论为我们的深度教学指明了方向。

关键字：深度教学  经验释疑  矛盾分析  动手操作  实践探索

一、经验释疑之深度教学

学生在学习活动中往往会产生各种各样的疑问，或许有的问题看起来是那么的幼稚，但是老师千万不能扼杀学生的这股质疑能力，要从生活经验出发去引导学生深入剖析这些问题。这样，在一次次的质疑及释疑声中，学生和老师都能得到更长远的进步。

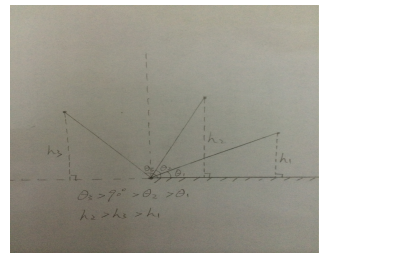
在一次课上，我让学生预习书上的“你知道吗”，这部分的内容是这样的：“放风筝比赛统一用30米长的线。在测量高度时只要将风筝的一端固定在地面上，然后测量风筝线与地面的夹角，夹角越大，风筝越高。”学生在读完之后纷纷表示不解：当夹角从0°增加到90°时高度是越来越高的，但是90°到180°时却是越来越低。下面是附上的草图：

带着这个疑问，引发学生更深入的思考：“换作是你，你觉得应该怎样表达更合适？”经全班交流之后，得出统一看法：夹角越接近90°，高度越高。

我对他们的探索过程和发现给予了肯定，不过接下来并没有急着给予评价，而是顺势展开了谈话。

师：“同学们，有自己去放过风筝的吗？请举一下手。”

所有的同学都高高举起了小手。

师：“我们去放风筝的时候，要始终注意风筝的状态，那么风筝是不是始终在你眼睛的斜上方？”

同学们点头。

师：“此时你觉得风筝线与地面的夹角，是应该量锐角还是钝角？”

同学们一致认可是量锐角。

师：“所以，风筝比赛的时候量风筝线与地面的所夹的锐角，夹角越大，风筝越高，并没有什么问题。”

同学们表示了释然。

是呀，生活经验是学生获取知识的重要途径，而这种基于生活经验的教学引导是很容易引起学生与旧知识的共鸣的。

二、矛盾分析之深度教学

生活中处处存在着矛盾，教学中也是。而抓住矛盾、转化矛盾往往能够解决很多的实际问题。在六年级的数学教学中存在着诸多知识重点、难点，分率、比的应用首当其冲，学生在相关知识应用中往往会出现思维疑点、难点，以分析矛盾为抓手的深度教学就势在必行了。

一次课上，我给学生们出示了这样一个问题：“男生与女生人数比是3:5，你能从中了解哪些其他信息？”同学们纷纷举手发言，有份数角度出发的“男生看成3份，女生看成5份，总人数看成5+3=8份，女生比男生多5-3=2份”；也有看出分率的“男生人数是女生的，女生人数是男生的，男生是总人数的，女生是总人数的”；更有一些看出了“女生比男生多，男生比女生少”等等。

从一个比中，我们很容易看出几个量占了多少份，也能够看出几个量涉及的一些分率，相关联的信息这么多，我们怎么才能从中找出有用的呢？我觉得，能展开联想去发现矛盾，会去分析矛盾才是关键。

比如说这一个例子——原来男生与女生人数比是3:5，后来转进5名女生，此时男生人数是女生的，请问原来有女生多少名？

这边题干仅仅是多了一个分率的信息，大致也能看出原来与现在的一些份数以及分率。那么多个已知条件，该如何去筛选分析呢？我们先从份数角度出发，罗列一下简单的份数关系。

这其实就体现出了多个矛盾：男生原来占3份，明明人数没有变化，怎么变成2份了呢；还有女生原来就占5份，这次明明人数有所增加，怎么还是5份呢；还有总人数应该也有所增加，份数怎么反而少了呢。

把这些矛盾转化了，解题思路也就有了。从比中看出的份数都是相对的，我们可以同步进行变化。既然男生的人数没有改变，那么他的份数最好就保持相同，取2和3的公倍数6份即可。这样，这几个量的份数可调整为

女生增加5人，增加了5份，那么每份数就是1人，所以原来女生有10人，解题完毕。这种方法仅仅是解决了份数变化不一致这个矛盾，解题思路就豁然开朗了。

那从分率角度出发，又该如何去分析呢？首先，原来男生人数是女生的，后来男生人数是女生的，虽然两句话中的单位“1”都是指女生人数，但值得注意的是，女生人数有所增加，单位“1”的量也发生了变化，这就产生了矛盾。只需要换一个统一的单位“1”即可。在整个问题情境中，只有男生人数没有发生变化，于是就将男生人数看作单位“1”，两个分率相应发生变化：原来女生人数是男生的，后来女生人数是男生的。这样女生增加的人数5人就对应了增加的分率，两者相除求出单位“1”即男生人数，原来女生人数是。这种方法仅仅是转化了单位“1”不一致这个矛盾，阶梯思路自然而然就清晰了。

可见，在数学学习过程中，矛盾分析转化也是一项十分重要的技能呀！

三、动手操作之深度教学

有这样一句话：“我听见了，但可能忘掉；我看见了，就可能记住；我做过了，便真正理解了。”我们的数学课堂，不应该局限于纸上谈兵，而应该是注重动手操作的课堂。

在教学《长方体和正方体的表面积》一课时，我让学生提前准备好硬纸板、长方体和正方体纸盒各一件。从长、正方体纸盒中学生感受到了它们面的特征及表面积的组成，慢慢地也了解了长方体和正方体表面积的计算方法。而硬纸板是让学生通过裁减、拼接制作长、正方体以便更深刻地了解它们的特征、展开图和表面积等相关知识。

在小组合作制作长、正方体的过程中，有一个小组迟迟没有完成。他们反映：在硬纸板上只剪下一个正方体的展开图的话，接头处根本粘不牢，很容易散开，为了粘牢只能在每个角落都多剪下来一点，不过此时不知道怎么算表面积了。

是呀，我们生活中只要涉及动手操作，都难免面对接头处该如何处理这个问题，逃不开也躲不掉。只有把这部分知识充分内化了，才能彻底解决这样的问题。

现在，我把生活中的一个常见问题搬到课堂上来让同学们充分思考：“长正方体的表面积都是指六个面的总面积，为了粘贴方便多剪下来的部分是贴合在里面的，并不算在表面积里面。我们生活中遇到的长正方体盒子，几乎都会有部分是贴合在一起的，就是为了使整个立体图形更加稳固。”

生活中类似的例子有很多,如：捆扎蛋糕盒，有接头处需要考虑；给木桶底面一圈安装一个铁箍，有接头处要考虑；这里的制作长、正方体纸盒，也有接头处需要考虑……通过这样的动手操作，发现问题并解决问题，让知识基于书本并超脱书本，真正做到活学活用！

四、实践探索之深度教学

知识来源于生活并应用于生活，记得很早以前就经常有小朋友喜欢来问我：金字塔的高度是怎么测量的呢？旗杆的高度可以用什么办法测量呢？我想知道这棵大树有多高可以采用什么办法呢？等等类似的问题。在六下学期学习完比例的相关知识之后，我把这几个问题重新抛给了这一届的学生，出乎意料的是，答案尽是钻牛角尖，真正可行的却屈指可数。这时候，要带他们真正体验一下数学实践的想法便萌生出来了。

课前我先做了一下简单的安排：①利用课间时间，两个同学一组，携带多个不同长度的物体，测量物体长度及影长并记录在表格中；②用计算器计算物体长度与影长的比值；③比较不同物体长度与影长的比值，交流发现；④在不同时刻重复上面三条，交流发现。

有了任务，同学们的学习热情空前高涨，不出1天，一张张实验记录表都已经登记完成。课堂上，多数小组都能得到类似于“同一时刻，不同物体长度与影长的比值相等”“不同时刻，同一物体的长度与影长的比值不等”等比较粗浅的结论。

师：“既然同一时刻，不同物体长度与影长的比值相等，那么也可以说是不同物体长度与影长——”

生：“可以组成比例。”

师：“而不同时刻同一物体长度与影长的比值都不相等了，说明——”

生：“太阳在慢慢地移动。”

师：“所以——”

生沉默。

师：“我们得抓紧时间去组成比例呀。”

（全班哈哈大笑）

师：“那我们可不可以利用咱们的探究成果想个办法测量金字塔、旗杆和大树的高度呢？”

生1：“我们可以带两把尺子量出尺子的影长，计算出尺子长度和影长的比值，再迅速去量出金字塔的影长，就可以利用比值相等求出金字塔的高度了。”

生2：“我们可以随便带上一个容易测量的物体，量出长度和某一时刻的影长，再量出大树的影长，将大树的高度设为x米，列出一个比例，解出这个比例就可以了。”

生3：“我要带一个卷尺去量旗杆的影长，记录下当时的时间，然后在第二天的同一时刻去量某个物体的长度和影长，组成一个比例，因为我觉得这样比较精确。”

……

同学们精彩的发言层出不穷，更有个别同学跟我说，他现在走在路上就特别在意路灯呀、电线杆、小高楼等，特别在意它们的高度，时而忍不住想去算一算；也有同学跟我说，他特别在意那些物体的影子，就担心没有正儿八经的投在地面上，导致不好测量……我想，这些同学此时的表现不就是数学知识作用于生活的结果么！

深度教学已经势在必行，如何在有限的时间和空间内提高教学深度，值得我们每一位老师认真推敲。贯彻陶老的生活教育理念，落实小学数学中的深度教学，让每一个学生享受学习，用心生活！

参考文献：

[1]倪兴奋.核心素养下小学数学教学深度学习策略实施路径探究.数理化解题研究，2020(11)：43-44.

[2]马银俊.深度学习理念下小学数学教学方法研究.科学咨询（教育科研），2020（02）：244.

[3]纪桂玉.“深度教学”让小学数学课堂回归本真.小学数学研究，2019（33）：71-73