《平面图形的周长和面积》

主备人：刘萍

【教学内容】教材第89～90页的“整理与反思”，“练习与实践”第1～7题。

【教学目标】

1.知识与技能：学生进一步理解和掌握平面图形周长和面积的含义，以及计算公式的推导过程；能正确运用公式计算周长和面积。

2.解决问题与数学思考：学生经历整理知识的过程，进一步构建知识网络，体会转化的思想及其价值；培养比较、归纳、推理等思维能力，发展空间观念。

3.情感态度与价值观：学生在讨论、交流中参与学习活动，进一步感受数学的应用价值，加强数学学习的兴趣和主动性。

【教学重点】平面图形周长和面积的计算公式的推导及其应用。

【教学难点】认识平面图形计算公式的内在联系。

【教学准备】师： PP课件

        生：课前回顾平面图形的面积公式及推导过程。

【教学过程】

一、复习导入

1.生活场景导入

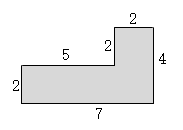（出示）这是公园里一处草坪的平面图，春天来了，工作人员要给这块地围上木栅栏，铺上草坪。你能提出什么数学问题？

（至少要多长的木栅栏？大约要铺多少平方米草坪？）

解决这两个问题和什么有关？

2.揭示课题

师：今天这节课，我们就一起复习平面图形的周长和面积。

板书：周长和面积总复习

二、复习周长和面积

1.复习含义

（1）提问：周长和面积一样吗？不一样在哪儿呢？

谁上来指一下？一起来描一描。

周长就是指围成平面图形的一周边线的长度。

板书：周长：一周边线的长度。

（2）提问：面积能这样指吗？谁来换一个手势？一起来感受一下。

面积就是平面图形的大小。

板书：面积：平面图形的大小。

2.复习周长的计算方法。

（1）列式解答第一个问题。

提问：你打算怎样解决第一个问题？需要哪些数据？给你测量的结果。

     现在你会计算它的周长吗？完成在学习单上。

（2）展示交流一：2+5+2+2+4+7＝22（米）你是怎样想的？

                 2×3+5+4+7＝22（米）你又是怎样想的？

     比较这两种方法，有什么相同之处？（都是将一周边线相加）

     我们从这将这个封闭图形的边线剪开，你有什么发现？（一周边线打开来成一条长线段）

     这条线段的长就是什么？求它的周长就是将所有边线长度相加。

其他平面图形的周长也能用这个方法解决吗？ 

（3）展示交流二：（7+4）×2＝22（米）和大家分享你的想法？（将一周边线转化成长方形的周长。）电脑演示转化过程。

通过转化我们将复杂的问题变得简单了。

刚才我们说平面图形的周长都可以将一周边线的长度相加，那长方形周长也可以用7+4+7+4？你为什么选择这种计算方法？

有些平面图形的边线比较特殊，我们研究时根据边线的特点，总结了一些平面图形周长的计算方法。想一想：我们还研究了哪些图形的周长计算公式？

（4）回忆特殊图形的周长计算方法。

正方形周长C=4a它的边线有什么特点？

圆的周长C=pd=2pr  它的周长指的是什么？（是一条曲线的长度）

（5）复习圆周长计算公式的推导过程。

圆的周长这个计算方法我们是怎样探究得到的？

提问：我们是怎样测量圆周长的？（将绳子绕圆一周，再拉直成一条线段，测量线段的长度，这是绕绳法；将圆在直尺上滚动一周，测量滚动的距离，这是滚动法。）

这两种测量方法中，有什么相同的地方？都用到了同一种数学思想方法——化曲为直。

测量出周长后，通过计算，我们发现圆的周长总是直径的p倍。所以计算圆周长可以用直径×p，或者半径×2p。

3.复习面积的计算方法

（1）列式解决第二个问题。

接下来我们该解决第二个问题了，你打算怎样解决？请在学习单上画一画，算一算。

交流解题过程。

比较这几种不同方法，有什么相同之处？（都将复杂图形分解成基本图形）

（2）复习面积计算公式。

在解决刚才的问题时，我们用到哪些平面图形的面积计算公式？是什么？其它图形的面积怎样计算？

（3）复习面积公式的推导过程

那这些面积公式我们是怎样得到的呢？请同桌两人相互说一说。

（1）长方形面积公式推导：

这是一个长方形，它的面积是长×宽，这个面积公式是怎么得来的？（给你一点小提示，这是一个面积单位的正方形。）从测量的角度就是看这个长方形里有几个这样的面积单位。

这里一排摆——5个，长就是——5，摆了这样的——3排，宽就是——3。

小正方形的个数=每排个数×排数，所以长方形的面积=长×宽。用字母表示就是S=ab。

（2）正方形面积公式推导

提问：正方形和长方形有怎样的联系？

当长方形长和宽相等时，它就成了正方形。正方形每条边的长度叫做边长。长方形的面积=长×宽，所以正方形的面积=边长×边长，字母表示就是S=a²。

根据正方形和长方形之间的联系，我们推导出了正方形面积计算公式。

（3）平行四边形的面积公式推导

提问：平行四边形的面积又和谁相联系呢？

沿着平行四边形任意一条高，都可以剪拼成长方形。

这样，我们就把未知的平行四边形面积转化成了已知的长方形面积来计算。

比较平行四边形和拼成的长方形，有什么联系？

平行四边形的底就是长方形的长，平行四边形的高就是长方形的宽。长方形的面积=长×宽，所以平行四边形的面积就=底×高。

（4）三角形面积公式推导

提问：平行四边形是这样转化的，那三角形又是怎样将未知转化成已知的？

我们把两个完全相同的三角形拼成了一个平行四边形。这样我们就把未知的三角形面积转化成为已知的平行四边形面积的一半来计算。

比较三角形和拼成的平行四边形，有什么联系？

平行四边形的面积=底×高，所以求其中一个三角形的面积就等于底×高÷2。

（5）梯形面积公式推导

提问：谁的面积公式的转化和它类似？

这样我们也把未知的梯形面积转化成已知的平行四边形面积的一半。

比较梯形和拼成的平行四边形，有什么联系？

平行四边形面积=底×高，而此时的底正好是梯形的上底加下底的和，梯形的高就是平行四边形的高，平行四边形的面积也就是梯形的（上底+下底）×高，那么要求其中的一个梯形的面积就是S=（a+b）h÷2。

（6）圆的面积公式推导

提问：圆是转化成什么图形来研究的？

我们把一个圆平均分成了16份，像这样剪开，再拼合，那我们就得到了个近似的长方形，当我们把这个圆平均分的份数越多时，那么拼成的图形就越接近于长方形。

这样，我们就把未知的圆的面积转化成已知的长方形的面积来计算。

比较圆和拼成的长方形，有什么联系？

长方形的长就等于圆周长的一半，等于pr，长方形的宽就等于圆的半径，长方形的面积=长×宽，所以圆的面积就等于pr乘r，也就是pr ²。

（7）形成结构

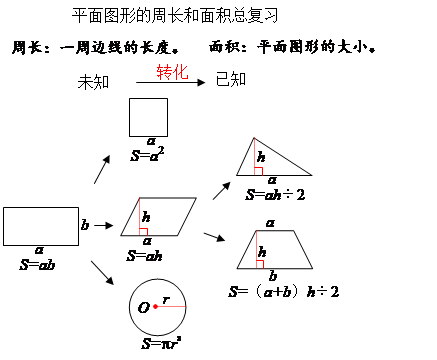
①提问：刚才，我们一起回顾了这六个平面图形面积的推导过程，请你仔细观察，哪些图形面积公式的推导过程有相同之处？什么相同？

板书：未知→已知

转化就是将未知转化成已知，利用知识间的联系，用旧的知识解决新的问题。

哪个图形不是这个方法，其他图形的面积也能用数方格的方法得到吗？

当我们得到长方形面积公式后，就可以将新的图形转化成已知图形来研究。长方形就是研究平面图形面积中最基本的图形，怎样摆放能让我们更清楚地看出这些图形中的联系？

通过刚才的复习，加深了我们对公式的理解，接下来老师要考考大家了，有没有信心接受挑战？

4.解决问题：

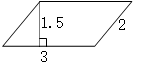
（1）计算下列图形的周长和面积。（单位：厘米）

 

 

 

 

提问：平行四边形周长为什么不加1.5？（不是边线），面积为什么不用2乘1.5？（对应）

 

 

 

（2）每组中的图形周长相等吗？面积呢？请在相应选项后的括号里画√。

 

 

 

 

 

 

 

 

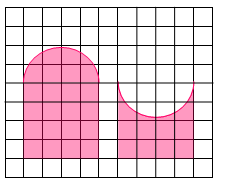提问：仔细观察这两幅图，你有什么想法？（面积相等的平面图形，周长不一定相等；周长相等的平面图形面积不一定相等。）

（3）那当两个平面图形相遇时，它们的周长和面积会发生怎样的变化呢？

出示：在一张正方形纸的外边上，剪下一个长方形，剩下的纸片的周长会发生怎样的变化？

交流展示：周长不变，周长增加，周长减少。

看来一切皆有可能！如果告诉你正方形的边长为10厘米，剪下长方形的长是6厘米，宽是3厘米，剩下纸片的周长最长是多少厘米？

这两种剪法有什么，有什么不同？又有什么相同？（面积相同）

变化中藏着不变，这也是数学的魅力所在啊！

三、全课总结

今天这节课，我们一起复习了哪些内容？

通过今天的复习，你又有哪些新的收获？

当遇到新的问题时，我们要想办法将它转化为已知的内容来解决，这样，我们掌握的本领会越来越多，思维会越来越灵活。

 

【板书设计】