课题：大树有多高              

【教学内容】教材第66—67页综合与实践“大树有多高。”

【教学目标】

1.知识与技能：学生能够运用所学的相关知识，主动探索并认识物体实际高度与影子长度之间的关系，学会综合应用所学的知识解决“大树有多高”这样的实际问题。

2.数学思考与问题解决：学生经历解决实际问题的过程，积累数学活动基本经验，进一步体会比和比例在生活中的应用价值，提高分析问题，解决问题以及应用数学知识的能力。

3.情感态度与价值观：学生感受到数学与现实生活的密切联系，进一步激发学习数学的兴趣，并在活动中培养创新意识。

【教学重点】认识并应用影子长度与物体实际高度之间的比例关系解决实际问题。

【教学难点】理解影长和实际高度之间的比例关系。

【教学准备】

    每组准备2把卷尺和4根竹竿：一根1米，一根2米，另两根竹竿长度不限，但要事先量好长度，并标注在竹竿上。每人准备—个计算器。

【教学过程】

 口算。

2013－619＝         7.24＋3.6＝       930÷31＝          2.4×0.2＝               

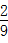×18＝            －＝          ÷＝            ＋＝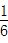

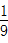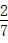一 、创设情境，提出问题。

（一)提出问题

1.创设情境。

谈话：(出示校园照片，突出一棵大树)同学们，这是我们美丽的校园，大家一起来看我们校园里的这棵大树。三年级的小朋友想给这棵大树做一张“身份证”，可是在填写这一栏时犯难了：怎样知道这棵树有多高呢?你们愿意帮助他们解决这个问题吗？

2.揭示课题。

揭题：今天这节课，我们就一起到室外进行综合实践活动，来解决这个实际问题：大树有多高。（板书课题）

3.明确要求。

提问：要使室外的实践活动有效进行，我们要注意些什么呢？

说明：到室外进行综合实践活动，首先，应围绕要解决的问题主动思考、互相交流，讨论解决问题的方法；第二，要按照找出的办法相互合作，分工负责完成操作活动，得到需要的数据；第三，要准确、清楚地记录、整理需要的数据；第四，服从班级、小组的集体活动安排，不做与活动无关的事情。

组织学生到室外活动。

(二)小组交流，提出猜想

    1．讨论方法。

    引导：仔细观察这棵大树及周边的环境，想一想，要知道这棵大树的高度，你想到哪些办法?在小组里讨论。

    交流：每个小组都想到了什么办法?把你们的想法与全班同学分享一下。

    学生交流，教师启发，引导学生了解不同的想法：

    (1)先了解附近建筑物的高度，再通过比较，估计大树有多高。

(2)可以爬到树上，用竹竿等工具想办法量出大树有多高。

(3)发现在阳光下，大树的影子长，小树的影子短；物体越高，影长越长，物体越短，影长越短。找一找树高和影长有没有关系，能不能利用关系求出树高。

追问：你认为哪种方法能方便和准确地求出大树的高度？

2.提出猜想。

引导：刚才同学们看到物体高，影子就长，物体矮，影子就短，认为物体高度与影长之间存在一定的关系。大胆猜一猜，物体高度与影长之间会有什么样的关系？

结合交流引导学生猜测出：

（1）物体高度与影长对应比的比值一定。

（2）物体高度与影长成正比例。

二、实验操作，比较发现。

1.测量比较。

引导：大家的猜测对不对呢？有什么办法可以验证呢？

活动：测量同样竹竿的影长。

（1）操作：各小组拿出1米长的竹竿，直立在地面上，测量并汇报1米竹竿的影长。

启发：比一比各小组测出的影长，你能发现什么?

(2)再次活动：各小组同时用2米长的竹竿直立在地面上，量出影长，比一比，你们又能发现什么?

 学生操作、测量，并交流影长。

提问：通过两次测量，大家能得出什么样的结论呢?

指出：同一时间、同一地点，相同高度的竹竿，影长也是相同的；2米竹竿的影长是1米竹竿影长的2倍。

2．测量计算。   

(1)活动：各小组任意拿出一根竹竿(各小组的竹竿尽量不要一样长)，同时直立在地面上，测出竹竿的影长井记录在课本的表格里。用计算器算出竹竿长度与影长的比值，得数保留两位小数。

每小组汇报测量与计算的结果，把每组的测量结果与计算结果填入表格里。

(2)提问：比较每次求得的比值，你有什么发现?我们原来的猜想对不对呢?

(3)小结：测量不同高度的竹竿和影长，可以发现竹竿的高度与影长的比值是相等的，也就是竹竿的高和影长成正比例。

三、应用规律，解决问题。

1.引导方法。

引导：同学们已经发现了物体影长与物体高度之间的关系，怎样利用这个关系帮助三年级的小朋友解决大树有多高这个问题呢？说说你的想法。

追问：测量哪些数据，就可以求出大树有多高？

2.测量填表。

测量：要求学生测量出一根竹竿的长度和这根直立竹竿的影长，以及大树的影长，并把结果填入第67页的表格中，完成后回到教室。

让学生回到教室，交流测得的三个数据。

3.解决问题。

引导：我们已经知道了表里的三个数据，根据前面物体高度与影长的关系，每个小组讨论一下，可以怎样求出大树的高度？

集体交流，引导学生理解可以根据竹竿高度和影长的比等于大树高度和影长的比，列出比例，解比例求出结果。

让学生列出比例解答，求出大树高度并互相交流。

4.完成小结。

提问：回顾一下，我们是怎样解决大树有多高这个问题的？这里应用了哪些知识？

小结：我们综合应用比和比例的知识，通过测量、计算求出了大树的高。在探索解决这个问题的过程中，先通过竹竿高度和影长的测量、比较，发现了在同一地点、同一时间物体的高度和对应影长比的比值是一定的，也就是它们成正比例关系。接着测量竹竿高度、竹竿影长和大树影长，根据对应数值成正比例关系，列出比例，再解比例求出了大树有多高。这里我们发现，平时一些不能直接解决的问题，综合应用数学知识、方法就可以获得解决。

四、拓展问题，延伸反思。

提问：同一棵大树，在不同时间它的影长会相同吗？说说你的想法。

那在不同时间物体的高度与影长的比会相同吗？为什么？在不同的地点呢？通过上面的测量、计算和思考，你能想到什么呢？

指出：在不同时间，物体的影长会变化的，所以用上面的方法测量、计算物体高度，要在同一时间、同一地点进行。在同一时间、同一地点测量，物体高度和影长成正比例，可以根据对应数值列出比例解决物体有多高的问题。

 

【板书设计】                大树有多高

 

在同一时间、同一地点测量，物体高度和影长成正比例。