公因数和最大公因数

【课前准备】

小正方形若干套。边长1厘米、2厘米、3厘米、4厘米、5厘米。

【设计理念】

1.设计体现学科育人，注重知识的整体建构，从唤醒因数的概念到引出公因数的

概念，再到联想公倍数的概念；注重学习方法的迁移，从本节课研究公因数概念的活动经验迁移至学习公倍数的研究方法。

2.通过铺图形引出新的数学概念，活动中逐步引导学生发现问题、提出问题、研究问题，并在研究时联系实际体会公因数的含义，从感性认知中生发理性思考。

3.注重思维可视化的展示，充分利用板书展示学生的思维和知识的关联。

 

课前情境创设：

师：在学习数学知识之前，我们先到兰兰家的新房参观一下，不错吧！其实这只是装修公司设计的3D装修效果图！

效果图中兰兰的钢琴背景墙打算使用正方形玻璃砖进行装饰，客厅的电视背景墙打算用正方形大理石装饰（本段录音）。今天我们这节课要请同学们帮兰兰家选材料的尺寸，有信心吗？

 

一、 初步感受：铺图形和因数的关系 

1.师：电视背景墙是个边长6米的正方形。用这6种规格的正方形大理石来铺，

为了便于研究，背景墙看作大正方形，大理石看作小正方形。哪种能将背景墙正好铺满呢？ 

师：同学们，怎样理解“正好铺满”？对，还要全部用一种规格的铺。

想一想或者算一算：边长几米的能正好铺满呢？ 

2.课件结合交流展示。

（1）每行铺了？个，铺了几行？师：你是怎么算的？的确正好铺满。

（2）每行铺了？个，铺了几行？师：你是怎么算的？

3.师：想到这4个答案的请举手，你们怎么一下子想到边长1米、2米、3米、6米的正方形能正好铺满的呢？不选4米、5米的呢？（板书1、2、3、4）

生：因为6除以1、2、3、6都能除得尽。联系上节课学的知识，还有别的想法吗？

也可以说1、2、3、6是6的？     4、5呢？是6的因数吗？铺时有剩余。

（同时闪除法中的1、2、3、6）

师：很会总结，用到了上节课中因数的知识来解释。是的，小正方形边长的米数是6的因数时，就能正好铺满。这4种规格的兰兰家可以选择。

录音：感谢同学们的建议，兰兰家将会根据颜色和美观程度作出最后的选择。请同学们再帮他们选一选钢琴背景墙的彩色玻璃砖的尺寸呢！

 

二、 活动探究：铺图形和公因数的关系

1. 出示例9：

师：哪种砖能将长方形背景墙正好铺满呢？ 

想一想、算一算，有困难的也可以借助手中的学具在研究单上铺一铺或画一画。四人小组开始吧。

2.交流：

（1）边长6分米的正方形能正好铺满吗？

生1 ：能。 师：你铺或者画了吗？那你是怎样想的呢？

生1：每行铺3个。你是怎么算的？18÷6=3

铺了2行。你是怎么算的？12÷6=2

的确正好铺满

（2）边长4分米的正方形正好铺满了吗？ 

生2：不能正好铺满。师：你是怎么想的？

生2：每排铺4个，还有剩余。用算式怎么表示？（铺一排，一个算式）

可以铺3行。用算式怎么表示？（再铺2排，一个算式）

不能正好铺满。

4.师：还有哪些边长是整分米数的正方形砖也能把这个长方形正好铺满？

生1：3分米。你是怎么想到的？

生：18÷3=6  12÷3=4

生2: 2分米。你是怎么想到的？

生：18÷2=9  12÷2=6

生1：1分米。解释一下？

5．师：为什么边长1厘米、2厘米、3厘米和6厘米的正方形砖都能正好铺满？（板书连线）同桌可以交流一下你的想法。

生：1、2、3、6既是12的因数，又是18的因数。

师：我们来看看图和算式，是不是这样？“既是”“又是”是什么意思？

这么简洁、凝练的总结，真了不起！

看来，只要边长的分米数既是12的因数，又是18的因数，就能正好铺满。

在数学上：1、2、3、6既是12的因数，又是18的因数，它们会是12和18的什么呢？

6． 4是12和18的公因数吗？为什么？（出示边长4的铺的那幅图）

4虽然是12的因数，但它不是18的因数，所以4不是12和18的公因数。

 

7. 回顾：同学们，刚刚我们进行了两次铺图形的研究，铺时我们都发现了问题；接着我们就提出问题：为什么有时能正好铺满?有时不能正好铺满？在研究和解决这个问题时，发现了公因数这个新知识。新的数学知识往往就要在这样研究过程中发现。既然我们知道了什么是两个数的公因数，怎么找两个数的公因数呢？

 

三、基于概念，自主探索，形成技能

师：比如：

1．出示例10：

师：先想一想：怎样的数是8和12的公因数呢？

用什么方法可以找到8和12的公因数呢？试试把找的过程写在研究单上。

   （2） 交流：

*分别列举出8和12的所有因数，再找一找（1、2、4上下合在一起1个椭圆圈，一共3个圈）……。这样就找到了8和12的公因数有1、2、4，其中最大的是4。

师：你是怎么想到先分别列举出8和12的所有因数，再找的呢？

*先找出8的因数，再从8的因数中找12的因数。（找的过程圈一圈）

师：为什么从8的因数中再找12的因数，就会全部找到了呢？

因为公因数一定在8的因数中。

*同样道理，也可以。先找出12的因数，再从12的因数中找8的因数。……

师：这些公因数中，其中最大的是4。4就是8和12的最大公因数。

那前面12、18的最大公因数是几呢？

揭题：这是我们今天学到的第二个新知识，最大公因数。

 

2．同学们表现这么出色，接下来奖励同学们玩个游戏：帮数找家。

（1）之前我们会用集合图表示一个数的因数，还记得吗？谁来分别把8和12的因数全部领回家。

 师：齐了吗？那怎么办？

（2）相机出示韦恩图。

（3）看得懂吗？5次亮图（8的因数、12的因数、8和12的公因数、8独有的因数、12独有的因数，师分别问：这表示？这表示？

（3）师小结：这就是数学的魅力，简简单单一副图就能表示出那么多的信息，掌声送给    。

3．小结：同学们，会找两个数的公因数了，还会用集合图来表示公因数了。带着这些经验，要请同学们帮我们学校出出主意了，这是我们学校的寻访活动，新一轮寻访活动又开始啦！

四、解决实际问题，深化认知。

1.播放寻访小队的视频。

五（1）班有15名同学报名了，五（2）班有25名同学报名了，将各班分成人数相同的小队去参加活动，每个小队可以有多少人？

（1）想一想：每个小队的人数必须满足什么条件呢？

（2）每个小队可以有多少人，就是求15和25的公因数。

在数轴上怎么找呢？

师：你是怎么找的？

在15的因数上画三角形，在25的因数上画圆。

15和25的公因数有1、5。

每个小队可以有1人、5人。

师：你有什么好建议？

 

2. 我们在数轴上找到了15和25的公因数，前面两组数的公因数也表示在数轴上。

师：请同学们仔细观察，你能发现什么？

（1）生1：每组都有公因数1。师：为什么每组都有公因数1呢？如果是别的两个数的公因数也有1吗？（结合因数的特征来思考，真不错！）

（2）生2：两个数的公因数的个数是有限的。师：很会观察和联系，因为一个数因数的个数是有限的，所有两个数公因数的个数也是有限的。

师：再请同学们观察最大公因数和它的因数，你们又有什么新的发现？（一次一对对的闪）

是啊，还有这么有趣的关系的啊！1、2、3、6是最大公因数6的因数；1、5是最大公因数5的因数；1、2、4是最大公因数4的因数。

小结：结合因数的特征，我们又发现了公因数这么多的特征。同学们，相关的数学知识联系起来想是不是有意想不到的收获呢？

3.解决实际问题。

这是教育局给我们学校配的采样小屋，有两个采样窗口，去采样的同学可以这样排成两队（采样小屋标出来）。左边小路的长度是42米，右边小路的长度是24米（标出长度）。前后两个同学之间的距离（整米数）要相等，前后两个同学之间的距离可以是多少米？ 

师：先想一想，间隔距离要满足什么条件呢？

※出示1米线贴好的样子。这就是常态核算采样的要求

※出示2米间隔的图，小圆圈代表人。这就是封控区核算采样的要求

※出示3米间隔的图，小圆圈代表人。

※出示6米间隔的图，小圆圈代表人。

师：问题解决了，可以有4种方案呢。

录音：感谢同学们提供这么多的好建议，我一定会向学校防疫小组转达同学们的好建议！

五、全课总结:形成知识结构图。

我们一起来回顾一下（课件4副图：因数、公因数、求两个数的公因数、公因数的应用）今天的学习过程，你有哪些收获？

1、最后运用新知求两个数的公因数和最大公因数，并解决了学校中的问题。

2、收获了研究生活中数学问题的一般步骤。   

 

今天我们研究了小正方形铺图形，如果有要用小长方形铺图形呢？哪种正好铺满？

师：两个数之间如果有因数的关系，就会有倍数的关系。其实在铺图形时有的同学还想到了倍数的知识，你又能联想到什么知识呢？

这就是我们下一节课要研究的内容。同学们可以试着用今天学到的方法先去研究一下两个数的公倍数。

 

六、手写板书。

   

板书：

铺图形

小正方形的边长

大正方形的边长

小正方形的边长

长方形的长

长方形的宽

除法算式

因数

倍数

公因数（这是标题字大点）

最大公因数（这是标题字大点）

2个数

3个数

发现问题（黄色的字）

提出问题（黄色的字）

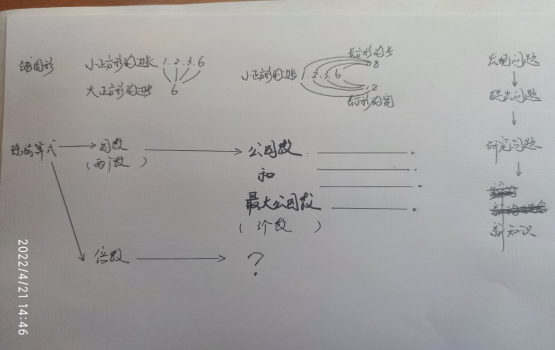研究问题（黄色的字）

 

 

 

 

预备课内容： 

1、练习8、12、18、15、25、24、42的因数。

学生的格式  8的因数（或直接8）：1、2、4、8。

2、聊一聊因数的特征：最小的因数是1，最大的因数是本身，因数的个数是有限的。

3、用边长1厘米、2厘米的铺一铺边长3厘米的正方形，问一问，为什么1的能铺满？      2的不能？

 

 

 

这是教育局给我们学校配的采样小屋，有两个采样窗口，去采样的同学可以这样排成两队。左边小路的长度是42米，右边小路的长度是24米。前后两个同学之间的距离要相等，前后两个同学之间的距离可以是多少米？