纠错：重在强化对概念本质的理解

                           —— 一道练习题的教学片断与思考    

 张皎（江苏省宜兴市实验小学）

 

 

苏教版五年级下册第六单元《圆》的“整理与练习”中有这样一道题：

 

 

 

在求运动场的周长时学生出现了这样的错误算式：3.14×64+（100+64）×2。

在平时的教学中，老师们也很注重周长与面积的比较，但在解决问题的过程中，学生还是会不时出现错误，尤其是周长的计算，如上述例子中，求运动场的面积正确率较高，可是在求运动场的周长时，就有学生很迷惑：“我用圆的周长加上长方形的周长，难道不对吗？”为什么求组合图形的周长容易出错呢？追根溯源，主要有以下的原因。

首先是对周长概念内涵理解不深入。概念是数学学习的基础，也是学生运用数学知识解决问题的关键。课堂上如果在概念构建的过程中浅尝辄止，忽视展开概念抽象过程，则学生对概念的理解往往浮于表面。而在新授课上得出求图形周长的公式后，师生又往往更注重于周长值的获得，解题过程一般就简化成了看到问题就直接套用公式求值，而淡化了“先找一周边线→再累计求和”的周长概念具体化的过程。若长时间缺失过程性经验的整理回顾，学生头脑中已经形成的周长表象就会逐渐弱化，对周长概念获得过程的记忆也将变得零碎、片面，导致与面积概念的表象互相干扰，意象不清。

其次是面积求和思维方式的负迁移。

不妨先理一理小学阶段周长概念的生长逻辑：苏教版教材在第五册安排了“认识周长”、“长方形和正方形的周长计算”的

教学，第六册安排了“长方形和正方形的周长与面积综合练习”，第十册安排了“圆的周长”、“圆的周长和面积综合练习”等的教学。可见，周长概念的学习主要在三年级，五年级下学期学完“圆的周长”后再次对周长知识进行综合应用。而四年级整个学年、五年级大半个学年是周长知识应用的一个“断层期”，尤其是五年级上学期在学习“多边形的面积”这个单元时，教学重点是多边形面积公式的推导过程，之后的练习也是关于多边形面积的综合训练。学生面积计算接触的多了，就产生了一种固定的思维模式。上题求运动场面积只要把各部分图形“面积求和”，这样的思维模式学生轻车熟路，而在求周长时模仿类推，导致出错。思维定势、经验定势、类比定势这些心理因素就导致了求组合图形面积的思维方式对求周长产生了负迁移。

因此，纠错要重在教学过程中强化对概念本质的理解。

    片断一：厘清本质，重塑概念意义

求运动场的周长出现了这两种算式：

①3.14×64+（100+64）×2。

②3.14×64+100×2。

师：你们有什么想说的？

生₁：3.14×64和（100+64）×2分别求的是圆和长方形的周长，这里的运动场是一个组合图形，它的周长就等于圆的周长加上长方形的周长。

生₂：我也同意第一种。

教师不多作评论，稍等片刻又有学生

陆续举手。

生₃：我觉得运动场的周长不包括长

方形的两条宽，（边说边跑到屏幕前用手

绕着运动场图的边线指了一圈），所以第二种方法才是正确的。

这一动作似乎勾起了其余学生对周长意义的回顾，纷纷赞同生₃的意见。

生₂：我有点疑问，为什么求运动场的面积可以用圆的面积加上长方形的面积，而求周长不能这样做呢？

师：那同学们想一想，什么是一个图形的周长？怎样才能得到一个图形的周长呢？

生₄：老师我知道，要得到一个图形的周长就要求出这个图形一周边线的总长，所以我们首先要找到一周的边线。

生₅：尤其是组合图形，我们可以先描出一周的边线，这样能更清楚地看出它的周长包括哪些边线的长度。

其余学生对该生的建议表示这是很有必要的一个审题过程，纷纷在数学书上描出运动场一周的边线。

生：现在我们就可以很清楚地看出运动场一周的边线包括长方形的两条长和两条半圆弧，所以它的周长就是长方形的两条长和一个圆周长的总和。

   生₂：我现在明白了，运动场的面积指的是这个组合图形整个面的大小，所以要用各部分的面积相加；而运动场的周长指的是它一周边线的总长，需要我们仔细看这一周到底包括哪些边线的长度，不能简单地认为也是各部分图形的周长相加。

师：看来求组合图形的周长并不简单，只有清楚了意义，才能用对方法。

【思考】学生只有把握了周长概念的本质，才能有效掌握并灵活运用周长计算的方法。苏教版三年级上册中并没有对“周长”下明确的定义，只是描述为“书签一周边线的长就是它的周长。”而高等数学中对“周长”有明确的定义：“环绕有限面积的区域边缘的长度积分，叫做周长。”把两种定义进行对比理解：“一周”与“环绕有限面积”说明了周长与面积都依存于封闭图形中；“边线的长”与“边缘的长度”说明了周长需要度量出边缘的长度，而后者中的“积分”两字则是说明了有时还需要把度量出的结果进行累加。                  

上面教学片断中，教师首先引导学生分析出现的两种算式中各部分的意义，触发学生自觉展开对学习周长过程性经验的整理与回顾，重现周长表象，借助运动场图直观地提炼出周长意义的核心——“一周”、“边线的长”，从而更清晰地把握概念的内涵，并将周长概念具体化为运动场一周的边线的长。接着学生通过指一指、想一想、描一描，清楚地看到了运动场的周长应该是哪些边线的长度累加得到。这一学习过程，进一步加深了学生对周长的理解，并有利于学生养成在图形测量计算时，首先应运用观察想象等将概念具体化，并逐步形成习惯。

片断二：变式比较，深化概念理解  

师：关于组合图形的周长，大家还有什么疑问吗？

生₁：是不是所有组合图形的周长都不能用各部分图形的周长相加或者相减呢？

一石激起千层浪，学生们展开了讨论，举例、争论、说理，黑板上先后呈现了这样三幅图（相同的长方形和两个半圆不同的拼组）：

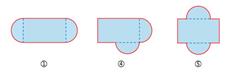生₂：其实组合图形的周长也可以先用各部分图形的周长相加减，只不过还要有一些后续步骤。比如图①涂色部分的周长如果用长方形的周长加上圆的周长，那就还要再减去不是涂色部分边线的长方形的两条宽；而如果是先用长方形的周长加上两个半圆的周长，那就还要减去长方形的4条宽了。

生₃：我听明白了，那么图②涂色部分的周长如果用长方形的周长减去两个半圆的周长，因为长方形周长里并不包含两条半圆弧，所以要得到涂色部分边线的总和就要再加上一个圆周长的两倍。

生₄：他们说的方法也是可以求出组合图形的周长的，但我认为这样做思考起来比较复杂，比如图③，简单的方法还是根据周长的意义先找出一周的边线，再把边线的长度累加求和比较容易思考。

包括生₂生₃在内的学生都倾向生₄所说的解题思路。

生₅：所以我认为在求组合图形的周长时不用纠结于到底能不能用各部分图形的周长相加或相减，只要“先找一周边线→再累计求和”，就能顺利地解决问题。

到此，学生对什么是组合图形的周长、怎样得到组合图形的周长已经在理解的基础上心中明了。进而，还有学生自然地把“周长”与“面积”联系起来。

生：从中我们还可以看出，面积大的图形周长不一定大。

生：是的。这三幅图的涂色部分，虽然面积不相等，但是它们的周长都可以把相同的两条长和一个圆周长累加得到，所以它们的周长都相等。

生：如果把图①中的半圆再换一下位置，还有可能涂色部分的面积相等，但周长不相等呢！（还是相同的长方形和两个半圆，黑板上又增加了几幅图）：

生：通过观察和比较，我们可以知道：前三幅图（指图①、②、③）的涂色部分是面积变了，周长不变；后三幅图（指图①、④、⑤）的涂色部分是面积不变，周长变了。

……

师：图形虽然千变万化，但只要真正理解了周长的意义，求组合图形的周长时就不会和求面积混淆，就能抓住关键，顺利地解决问题。

【思考】变式与比较是深化对概念理解的重要方法。上述教学片断中，学生在教师的启发下，质疑：是不是所有组合图形的周长都不能用各部分图形的周长相加或者相减呢？全班学生由此展开了讨论。讨论中，学生主动将运动场图进行变式，并根据周长的含义灵活运用方法解决问题。在此基础上，通过比较，异中求同进一步领悟到：求组合图形的周长时不用纠结于到底能不能用各部分图形的周长相加或相减，只要“先找一周边线→再累计求和”，就能顺利地解决问题。而后学生又再一次把运动场图变式，自然地把“周长”与“面积”联系起来，在“变”与“不变”中进一步深化了对周长概念的理解。

针对求“运动场周长”的错例，教师没有就题论题，也没有限制学生的思维宽度，而是围绕强化对概念的理解，让学生表达出各种思路去反思，去透过现象梳缘由。理越辨越明，道越论越清，不同想法之间辨一辨，课堂不失精彩、学生不乏兴趣。利用错误资源，化弊为利，就能取得理想的教学效果。

有人说，出错是发展中的学生的权利，学生对于知识的正确掌握往往是在“发生错误→（在教师的引导下）研究错误→改正错误”的过程中实现的。纠错，重在让学生强化对概念本质的理解，真正地学深悟透，方能斩草除根事半功倍。