促进深人思考,发展高阶思维

——《小数乘小数》教学与思考

张皎,褚明月
(江苏省宜兴市实验小学,214200)

摘要:教学《小数乘小数》一课,基于之前的学习经验,学生理解算理与掌握算法的难度不大,但是,教师不能以强化技能训练为主,使学生的思维处于“低阶状态”,而应促进学生深入思考,发展学生的高阶思维。具体地,可以让学生在提出问题、推理解释、一题多解中深入思考。

关键词:高阶思维 提出问题 推理解释 一题多解 《小数乘小数》

 

“小数乘小数”是苏教版小学数学五年级上册第五单元的内容。这部分内容是在整数乘法、小数乘整数、积的变化规律等内容的基础上教学的。基于之前的学习经验，学生理解算理与掌握算法的难度不大,那么,我们的教学能否以强化技能训练为主呢？显然,如果教学的视角局限于此，那么,学生的思维就会单一、定式,处于“低阶状态”。如何体现计算教学的价值,促进学生深入思考,发展学生的高阶思维,从而达成计算教学基础性和发展性的和谐统一？我们开展了如下的实践与思考。

一、在提出问题中深入思考

师：小明家打算购买一套新房。(出示图1)看!这是新房的部分平面图。根据图中的信息，你能提出哪些数学问题?

 

生：阳台的面积是多少平方米?

生：卧室的面积是多少平方米?

生：衣帽间的面积是多少平方米?

生：阳台、卧室、衣帽间的面积一共是多少平方米?

生：卧室的面积比阳台大多少平方米?

生：衣帽间的面积比卧室小多少平方米?

师：看来能够提出不少数学问题呢!先来看同学们已经提出的这些问题。你能解决哪些问题?

生：衣帽间的面积我会算,0.98×2,只要按照学过的小数乘整数的方法计算出结果即可。

生：衣帽间的面积我也会算。但求阳台的面积要用1.15×3.2,求卧室的面积要用3.8×3.2,两个乘数都是小数，我还不太会算。

师：这些都是一步计算的问题，还有几个问题,你们是什么想法?

生：只要知道阳台、卧室和衣帽间的面积分别是多少,就能求出它们一共的面积和相差的面积。

生：我觉得,求这三个地方一共的面积没什么用处,这个问题没有必要提出来。

生：我赞同,有时候提 出的数学问题并不是越多越好。

……

(教师最后在黑板上留下三个问题:①衣帽间的面积是多少平方米?②卧室的面积是多少平方米?③阳台的面积是多少平方米?)

就学生数学学习的思维层次来说，提出问题比解决问题层次高。发展学生的高阶思维，要引导学生从具体情境中提炼出数学问题，并进一步启发学生的思考由浅人深、由表及里。

上述教学片段中,數师从“你能提出哪些数学问题?"出发.开启学生的思考,让学生养成“数学地”看待生活实际问题的意识。此时,学生的思维是浅显的、零散的，他们只是习惯性地把能想到的问题都尽量提出来。接着,教师通过“你能解决哪些问题?”这一-导引提问，让学生进一步调动知识储备,针对几个能一步计算的问题明确已知与未知。最后,教师利用“还有几个问题，你们是什么想法?”推进学生深人思考,让学生意识到所提问题的相互关系和思维价值。可以说，正是教师提出的三个层次性问题，引导学生不断找到思考的增长点,相互辨析、纠偏、补充、完善，获得思维进阶。面学生思辨之后留下的三个数学问题又具有层次性:对应的三个算式0.98×2、3.8×3.2、1.15×3.2,分别是小数乘整数、小数乘小数、积需要化简的小数乘小数。面依托已有知识和经验探索新问题的解决之道,正是课堂教学接下去的任务。

 

二、在推理解释中深入思考

师：先来算一算卧室的面积。3.8×3.2的积是多少?试试看。

(学生尝试计算后展示汇报,出现如图2所示的两种情况。)

师：哪个结果正确?说说你的想法。

生：我认为121.6正确,我算出的就是这个结果。因为两个乘数都是一位小数,所以积也应该是一位小数。

生：我认为12.16正确。因为第-一个乘数是一位小数,第二个乘数也是一位小数,1+1=2,所以积应该是两位小数。

师：咱们来观察一下这两个竖式计算过程。显然,有了前面的学习经验,同学们都自觉把小数乘小数转化成了整数乘整数。善于迁移，真棒!因此，问题的关键在于确定积的小数位数。对此,谁能做出合理的解释?

生：我认为这里的积不应该是121.6。我计算前估计了一下结果:把3.8看成4,4×3.2=12.8,所以积不可能是100多。

生：对呀,对呀! 我们也可以把3.2看成3估计结果,即3.8×3=11.4；还可以把3.8×3.2看成4×3,估计出结果是12。这样的话,积只能是十几。

生：(之前做错的学生)现在，我也认为积不应该是121.6了。以后,我也要在计算前先估计一下，或者在算出得数后估算一下结果是否合理。

师：看来,不论计算前还是计算后的估算，都能帮助我们提高计算的正确率呢!这里的积应该是12.16,是两位小数。对此，你们能够做进一步的解释吗?

生：因为计算时,我们把3.8×3.2看成38×32,两个乘数都乘了10,所得的积就等于原来积的100倍；原来积的100倍是1216,所以,要得到原来的积，就要反过来把1216除以100,也就是从右边数出两位，点上小数点,积应该是两位小数12.16。

(教师相应地板书,如图3所示。)

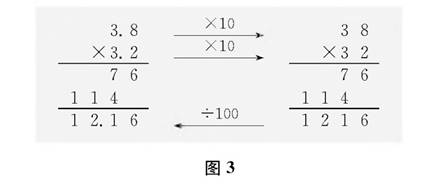
师：通过推理，我们证明了3.8×3.2=12.16,和估计的结果是一致的。

生：我原来算的积也是121.6。通过反思，我现在明白了小数乘小数的计算道理。之前学过的小数乘整数和今天学习的小数乘小数都可以先转化成整数乘整数来计算，但是小数乘整数的转化过程中，只有一个乘数发生了变化,积的变化只受这一个乘数的影响;而小数乘小数的转化过程中,两个乘数都发生了变化，所以积的变化就受两个乘数的影响啦!

生：看来,乘数中一共有几位小数,积就有几位小数。

师：同学们在学习中善于反思、勇于批判,令人欣喜。下面，就用刚刚探究出的小数乘小数的计算方法来算一算阳台的面积吧!

(学生尝试计算。)

生：我先估算了一下，积应该是3点多。我算出来的是3.68。

生：我算出来的也是3.68。但是,我有疑惑:之前我们发现,乘数中一共有几位小数,积就是几位小数,可是,这里的两个乘数中一共有三位小数,积却是两位小数,这是为什么呢?

师：这与我们之前的发现产生了一些矛盾。难道之前的发现不对吗?谁又能做出解释呢?

……

理解算理，才能牢固掌握算法。而经过推理(也就是寻找道理,做出解释)，才能真正理解算理。尝试推理,包括合情推理和演绎推理,是发展学生高阶思维的应有之道。小学生的推理,通常不能一蹴而就,需要在思辨中完成,从而培养思维的灵活性、深刻性和批判性。

计算小数乘小数时,依靠经验和直觉,按照整数乘法算出积后，如何回归小数乘法的积，即确定积的小数位数,是学生思维的主要困惑处。对此，教师没有直接肯定或否定学生的简单猜想，而是不断鼓励学生尝试推理,“做出合理的解释”。在计算卧室面积时,学生内思外辨,从合情推理到演绎推理,在自我反思与批判中意识到估算的重要性,沟通了小数乘整数与小数乘小数的联系，进而循着算理发现算法。在计算阳台面积时,由于结果进行了化简,导致与之前初步建立的算法产生了矛盾,于是，再次引发学生尝试推理，“做出解释”。这里,教师的“审问”，使学生“慎思”一学会周全地思考；又引发了学生的“审问”,让同伴“明辨”一形成清晰的判断。这是一种真正的“数学行走”,促进了学生高阶思维的发展。

 

三、在一题多解中深入思考

(教师出示练习:小明家打算购买的新房总面积是100.5平方米,每平方米的售价是1.2万元，小明的父母共有110万现金,买这套房子够吗？房款一共是多少万元?)

师：我们先来解决第一个问题。大家可以想一想,也可以算一算。

(学生思考、计算。)

生：解决这个问题，估算一下就可以了。把100.5看成100,1.2看成1,100×1=100,所以买这套房子110万够了。

生：解决第一个问题的确只需要估算一下,但是，如果把两个数都看小了,那么误差相对会比较大；而且，这样估算的结果是偏小的，也就是说，实际房款是大于100万的，所以,我们不能肯定110万就够了。我们可以只把100.5看成100,100×1.2=120,所以，买这套房子需要的钱比120万还要多一些，110万是不够的。

师：还有哪些同学也选择了估算方法来解决这个问题的?

(全班学生几乎都举起了手。)

师：大家能够根据需要选择合适的计算方式解决问题,很好!但是,为了不影响对结果的判断，要尽量减少估算的误差,还要明确估算结果相对于实际结果的大小。

生：我同意第二个同学的估算方法。我想说的是,如果全部用现金，110万元是不够的；但是，如果小明的父母可以用公积金贷款买房，那么，有110万也够了。

生：要是这样说的话，还可以向亲戚朋友借款啊!师你们能够与时俱进地思考问题,很好!但是，根据问题的情境描述,我们不考虑贷款或借款的因素,那么,110万现金是不够的。要想确切地知道买这套房需要多少钱,可以怎么办呢?

(学生动笔计算。)

生：(出示计算过程,如图4所示)我是列竖式计算的。

师：计算很细心,最后还注意了结果的化简。

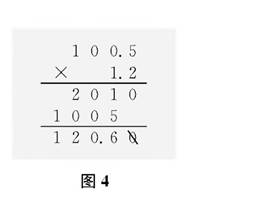
生：之前估算时已经得出了100×1.2=120,所以我再算0.5×1.2=0.6，120+0.6=120.6。师计算时巧妙地运用了乘法分配律,是个爱思考的孩子!对于0.5×1.2=0.6,你是怎么想的呢?

生：我是想0.5×1.2的结果就是1.2的一半，1.2+2=0.6。这样,每一步都只需要口算就行了。

师：原来计算0.5×1.2时,你是把乘法转化成了除法。像这样的小数乘法计算,我们下节课会重点研究。

生：如果有计算器 ,还可以用计算器来计算。

师：是的。遇到数目比较大的计算,可以借助计算器。我们要根据实际需要,选择合适的计算方式。

一题多解,即对一个问题进行多角度、多侧面、多层次、多结构的分析,是学生发展高阶思维的重要标识。为此，教师要创设具有开放性的问题情境,引导学生多方探索、深入思考,触类旁通、不断勾连。

上述教学片段中,出示巩固练习后，教师没有用“估算”“精确计算”“口算”“列竖式计算”等提示语限制学生的思路，而是让学生自主选择计算方式。因此，学生解决问题时出现了多样的算法，并且明确了各种算法的适用情况和注意事项。其中,利用乘法分配律口算的方法无疑令人眼前一亮:算起来简便,知识运用上承前(100×1.2=120是小数乘整数)启后(0.5×1.2=0.6是小数乘小数)。此外，还有学生打破固有的模式,给出了创新的思考:用公积金贷款或向亲戚朋友借款;用计算器计算。这些都是灵活、发散的思考,虽然与本课教学甚至数学教学关系不大，但是,拓展了教学的视角,也很有价值。教师没有强硬否定,而是温和保护、巧妙引导，从而让学生的思维得到更深、更广的发展。