
加入时间:2022-05-25
加入时间:2023-10-30
加入时间:2022-05-25

加入时间:2022-05-25
加入时间:2022-05-25

加入时间:2022-05-25

加入时间:2022-05-25
加入时间:2022-05-25

加入时间:2022-05-25

加入时间:2022-05-25

加入时间:2022-05-25

加入时间:2022-05-25
加入时间:2022-05-25

加入时间:2022-05-25
体育课上的“数学味”
——对体育中数学问题的思考探究
丁山实验小学 周佳伟
【摘要】生活是最好的学习素材,它是多门学科的一个综合。为了更好地适应未来课程发展的需要,也为了让我们国家的教育更好地走向国际化,融合课程一词应运而生。本文将重点探究数学与体育的融合,以此寻找两门学科之间的契合点,从而展开论述。在我看来体育之中也处处充满着数学,由此,可以从中发现一个个数学问题。通过对体育课中的一个个数学问题进行分析,得到的结论还可以运用到生活之中,也就很好的实现了学以致用。
【关键词】体育 数学 数 形
帕斯卡尔说过:“人是一根会思考的芦苇。”这告诉我们人是会去系统地思考的,也时刻提醒着我们要不断地思考进取。而作为一名数学教育工作者,更应该深思熟虑,才能更好地去教书育人。但是光思考数学当然是不行的,这样没有办法教好数学,一定要从生活中去发现数学之美,甚至可以从其他的学科里发现数学问题,从而引发思考。
在生活中人们总是会把一句玩笑话挂在嘴边,“你数学是体育老师教的啊”,但其实玩笑归玩笑,各学科之间不应该有明确的界线,往往体育课中也蕴含了许许多多的数学知识,细细品味起来还是有很多大学问的。
一、“数”的问题,有理有据
我们先来看一下历史上著名的“点人数”问题,这个问题被记载在一千多前的《孙子算经》中:现在有一个不知道等于几的数,这个数除以三余二,除以五余三,除以七余二,问这个数是多少?而体育课中也会有类似的问题:某一天上午第三节体育课,我们学校一二班的孩子下去上课,由于体育老师第一次给这个班级上课,他很好奇想知道这个班级的人数,但又不想直接通过“数”的方法,于是做了以下事情:让3人站一列,多出2人;让5人站一列,多出2人;让7人站一列,多出5人,这个时候他立刻就知道了这个班级人数是47人。
那么,问题来了,体育老师是怎么知道人数的呢?我们把他的做法转化成数学问题:3人1列多2人就是除以3余2,5人1列多2人就是除以5余2,7人1列多5人就是除以7余5,这个数可能是多少?对于这类问题,我们最先想到也最常用到的解决方法就是列举法。
列举法:(列出所有可能的情况)
① 除以3余2的数可能有:2、5、8、11、14、17、20、23……44、47、50……
② 除以5余2的数可能有:2、7、12、17、22、27……42、47、52……
③ 除以7余5的数可能有:5、12、19、26、33、40、47……
到这里的时候,我们就可以发现47是除以3余2,除以5余2,除以7余5三个条件都满足的,但是是不是只有47才满足这三个条件呢?当然不是,还有其他的数字也会满足这三个条件,比如152,只不过考虑到一个班级的人数情况,47当然是最好的答案。
关于列举法的另外两点思考:
a.既然除以3和除以5都是余2,那么我们就可以想到3和5的最小公倍数15,因此,这两个条件可以转化成一个条件,那就是除以15也余2。
b.一个数要满足三个条件,我们可以先看第三个条件除以7余5,因为7的“跨度”相对于5和3要更大,先列举出除以7余5的数有:5、12、19、26、33、40、47……这样再一个数一个数地观察是否满足另外两个条件。
综上两点思考,我们可以得出更好的解法:
① 
|
 除以3余2的数
除以3余2的数
② 除以5余2的数
而除以15余2的数可能有:2、17、32、47、62……
其中我们发现只有47同时满足除以7余5,所以47是满足题意的。
在发现了这一规律之后,我们其实可以将其运用到体育课甚至其他的领域中。比如开运动会的时候人数较多,可以用于检查人数,或者检查体育用品如篮球的个数,工厂里检查砖瓦的数量……
二、“形”的问题,形象直观
〈1〉室内体育课趣闻
某天下雨,体育课只能改在室内上了。为了丰富孩子们的体育知识,体育老师就给孩子们讲有关奥运会的小故事,其中就讲到了奥运会的五环标志,如图1:
 图1
图1
当时,我正好也在教室,看着这个奥运五环,突然就想到了一些问题:这个五环图案能一笔就把它画出来吗?换作是其他图案的话,怎么判断能不能一笔把它画出来?
问题在提出来之后,我们首先要理解什么是“一笔画”?通俗的说法就是每条线都必须画出,且每条线只能画一次,不能重复。
这样看来,“奥运五环”完全是可以一笔画成功的,那么其他的图案呢?我们不妨再来看几个例子,如下图
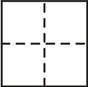
![~}]3E7Y26Y)KDU)EM`%@@TV](/ewebeditor/uploadfile/20250331094312871115.jpg)


图2 图3 图4 图5
经过一番探索之后,我们发现“田”、“品”“目”不可能一笔画成,而“中”字却能够一笔画成功,那能一笔画的图案有什么特点呢?首先,我们需要知道一笔画可以分为两种情况:一笔画终、起点不重合的情况,如“中”字;一笔画终、起点重合的情况,如“奥运五环”。然后,观察到每个点,可以将一个图形上的点分成两类:如果以某点为端点出发引出的线有偶数条,就称该点为偶顶点;如果以某点为端点出发引出的线有奇数条,就称该点为奇顶点。
接下来让我们分析:除去起点和终点两个点外,其余每个点,画一条线进去,就必然要画一条线出来,从而都必须是偶顶点,于是“一笔画”的必要条件是“图形中的奇顶点的个数为0或2”。也就是说,如果图形中的奇顶点的个数为0或2,就一定能完成一笔画。当图形中有两个奇顶点时,两两组合一下,以其中的一个为起点,另一个为终点,相信就能一笔画。但是当图形中没有奇顶点时,从任何一个点起始都可以完成一笔画,同时我们需要注意不会只出现一个奇顶点,因为每条线有两个端点。最后,我们知道:一笔画的充分必要条件是图形中的奇顶点的个数为0或2。
〈2〉期末体测
时间过得真快,转眼已经到了学期末了,学校为了检测学生一学期的锻炼情况,打算给学生来一次全方位的检测,其中,立地跳远也就成了必考的项目。但是,由于平时缺乏对腿部力量以及跳远技巧的训练,所以相当多的孩子是随便跳的。他们中的许多人跳完之后看了表格,立刻就知道了自己的成绩,不过问题却出现了,有一部分孩子对自己的成绩并不满意,他们觉得自己能够跳的更远,可是成绩偏偏就很差,这又是为什么呢?体育中跳远是怎么测量距离的呢?怎么样才能跳的更远呢?先来看下面这个图:
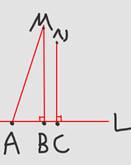 图6
图6
假设起跳线是直线L,一个同学从A点开始起跳(两脚并拢都在A点),双脚跳的一前一后,一只脚后跟在M点,另一只脚后跟在N点,试问线段MA,线段MB,线段MC哪个才是该同学的需要测量的成绩距离?
我们来分析一下:MA与MB都是一条线段,关键是问题,问题要求的是跳远的距离,试想一下,如果我们过M点作一条与直线L平行的直线L’,直线L’与L之间的距离就是垂直线段的长度,也就是线段MB的长度。或者简单一点讲点M到直线的距离是从点M到这条直线所画的垂直线段的长度。不过由于该同学两只脚一前一后,根据比赛规则,必须测量的是离起跳线最近的那只脚到起跳线的距离,因此,该学生的最终成绩实际上只是线段NC的长度,可想而知,该学生的成绩也确实不那么好了。
那么问题又来了,怎么样才能在肌肉力量,技巧都确定的情况下跳的更远呢?如图7
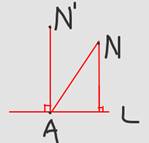 图7
图7
试想一下,该生还是从A点起跳,他如果斜着跳出去到任意点N,则该考生的成绩就是过点N向已知直线L作的垂直线段的长度;如果该考生笔直的跳出去到点N’(此时线段AN’与直线L垂直),则该考生的成绩就是线段AN’的长度,很明显成绩会比之前斜着跳出去好。又由于点前面已经说过是任意点,因此,笔直的跳出去成绩将会是最好的。
综上所述,要想在体育课最后期末测试的时候跳好要注意两点:1.双脚并拢跳出去,保证只有一个落脚点。2.笔直地用力地跳出去,尽量不要偏左或者偏右。
数学是什么?数学是研究一些数量关系与空间直观的一门学科。有人经常抱怨说:“数学咋看之下好像和生活不沾边。”事实上,那是因为数学把生活中的情境抽象出来了,数学是以强大的生活为背景的,但是,我们只看到那几个数字,却没有看到数学背后的东西,如果我们把视野放宽些,我们就会发现生活中处处都有数学。当然,生活不只是只有数学,它是众多学科的一个综合体,学科之间有时候没有清晰的界线,体育和数学也是如此,强身健体和思维训练可以同时进行,有时需要把它们看成一个整体,用系统多元化的角度来思考,来进步。
另外,在教学时应该从关注一堂课如何教,到走向一门学科如何教,只有树立了这样的“大课程”观,我们才能跳出繁杂的课程、课时限制,为学校发展、教师成功、学生成长奠定坚实的基础。