【教学内容】: 苏教版《义务教育教科书 数学 六年级下册》第七单元第78～79,练习与实

践1～5题。

【教学目标】：

1、进一步明确解决问题的一般策略，能按照一般步骤解决实际问题，了解小学阶段学习的策略，能应用从条件想起或者问题想起分析数量关系并列式解决。

2、能根据解决问题的需要，恰当选用不同的策略进行思考；能根据具体的问题灵活确定解题思路，合理选择解题方法，有效解决问题。

3、在运用策略解决问题的过程中进行合理灵活的思考，并清晰地表述自己的想法；具有主动运用策略解决问题的意识，体验解决问题策略的多样性，提升对解题策略价值的认识。

【教学过程】：

一、整理与反思。

1、回忆：解决问题的一般步骤是什么？

2、板书：理解题意(明确已知条件和所求问题)、分析数量关系(确定先算什么，再算什么)、

求出答案、检验反思。

3、回忆：我们在解决问题时，常常需要使用一定的策略，想一想，我们以前学过哪些解决问题的策略？

4、板书：从条件出发、从问题出发、画图、列表、列举、转化、假设。

5、回忆各种策略的具体应用。

（1）列表、画图策略。

小芳家栽了3行桃树、8行杏树和4行梨树。桃树每行7棵，杏树每行6棵，梨树每行5棵。桃树和梨树一共有多少棵？

小宁和小春共有72枚邮票，小春比小宁多12枚。两人各有邮票多少枚？

(2)从条件出发、从问题出发策略。

①小猴帮妈妈摘桃，第一天摘了30个，以后每天都比前一天多摘5个。小猴第三天摘了多少个？第五天呢？

可以从条件开始想起，确定先算第二天摘桃的个数，再算第三天摘桃的个数......

②一条裤子的价钱是48元，上衣的价钱是它的3倍，买一套衣服要用多少元？

可以从问题开始想起，确定先算一件上衣的价钱，再算一套衣服的价钱。

(3)列举、转化、假设。

6、小结：要选择策略，综合运用策略解决实际问题。

二、练习与实践。

1.做第1题，学生独立完成。

结合从条件想起，和从问题想起让学生具体说说“怎样想的？”

(1)买6件同样的短袖衬衫要用510元,每件长袖衬衫比短袖衬衫贵42.5元。长袖衬衫的单价是多少元/件？

从条件想起：总价÷数量＝短袖单价，先算短袖衬衫的单价.

(2)买6件同样的短袖衬衫要用510元如果用这些钱去买长袖衬衫，就要少买2件。长袖衬衫的单价是多少元/件？

从问题想起：总价÷数量＝长袖单价，先求长袖衬衫的数量。

明确：从条件想起，要找有联系的条件想能求什么，要先求什么，再求什么；从问题想起，要根据问题想数量关系式，看哪个条件还不知道，确定先求什么，再求什么。

有时候从条件想起比较方便，例如第1题，有时候从问题想起比较方便，解答时要同时联系条件和问题，一步一步思考，有时候两种方法是结合在一起思考的，不必截然分开。

2、做第2题，学生独立完成。

（1）学生分析，评讲。

（2）小结：总路程＝四季亭到月亮湖的路程＋月亮湖到盆景园的路程

总路程＝小芳行的路程＋小军行的路程

两题求的都是路程，数量关系是“路程=速度×时间”，但在具体问题是要结合条件和问题灵活应用数量关系，比如相遇问题，通过画图可以看出可以先求两人路程的和，也可以用速度×时间，思考过程不同，但它是符合乘法分配律的。

3、做第3题，学生独立完成。

(1)学生分析，评讲。

(2)小结：找准问题要求的年级的对应的行数和每行人数，用行数×每行人数＝年级总人数,求出所需的年级总人数。

4、做第4题，学生独立完成。

（1）学生分析，评讲。先让学生说说不同的思路，两种解法分别先求什么，再求什么？

(2)分析方法：

思路1:先求行驶400千米的耗油量,再与50升汽油进行比较。

先算行驶1千米的耗油量。1.2÷10×400=48（升）50＞48答：够行驶400千米。

先算400千米是10千米的几倍。400÷10×1.2=48（升）50＞48答：够行驶400千米。

思路2:先求50升汽油可行的路程,再与400千米比较。

先算1升油可行的路程。10÷1.2×50=416 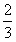（千米）   416 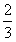＞400 答：够行驶400千米。

先算50升是1.2升的几倍。50÷1.2×10=416 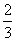（千米） 416 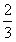＞400 答：够行驶400千米。

(3)小结：解决这题可以用归一或倍数关系解答。

4、做第5题，学生独立完成。

（1）提问：你是怎样分析这道题目的？让学生分析，评讲。

（2）全班交流：可以用列表摘录条件和问题，第一题根据工作效率不变，第二题根据工作总量不变来解答。

三、全课总结

今天我们主要运用了什么策略来解决问题？

从条件出发、从问题出发