圆的周长、面积计算练习

【教学内容】：苏教版义务教育教科书《数学》五年级下册第101页练习十五第10~15题，思考题

【教学目标】：使学生进一步掌握圆的周长和面积的计算，能根据条件计算圆的周长和面积，以及圆的组合图形的面积，以及圆的组合图形的面积，能解决一些圆的周长和面积计算的实际问题。

使学生能根据图形的特点和问题，正确选择条件计算周长或面积，进一步体会圆的半径、直径和周长、面积之间的联系，提高分析问题、解决问题的能力、发展空间观念。

使学生进一步体验圆的知识与现实世界的联系，感受平面图形的学习价值，培养应用意识，提高学习数学的积极性。

【教学重点】：

圆的周长、面积计算

【教学难点】：根据不同条件和图形特点选择正确计算方法

【教学过程】：

1.05÷3＝ 　　　   12.6－0.9＝         0.72+3.7=          10.1+1.01=

0.55＋2.45＝       2×0.25＝  　　　   80.8÷4＝          0.1÷2=

一、揭示课题

 谈话我们这个单元学习了圆的知识，学会了圆的周长的面积的计算。今天，重点练习圆的周长和面积的计算。（板书课题）通过练习进一步熟练圆的有关计算，能根据条件计算圆的周长和面积，应用圆的相关计算解决一些实际问题，提高应用知识的能力。

二、 基本练习

回顾方法

提问：圆的半径、直径和周长之间有什么关系？半径跟面积呢？

说明：根据圆的特点和周长计算，我们知道：直径是半径的2倍，周长是直径的π倍；反过来，周长÷π等于直径，直径÷2就等于半径。圆半径平方的π倍求出的就是圆面积。（板书：如下）

     ×2            ×π

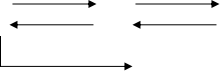r             d              c

 

     ÷2            ÷π

         S=πr         

 

那根据上面这样的关系，圆的周长要怎样计算？面积呢？（板书：C=πd  C=2πr       S=πr²）

2.分别计算下面各圆的周长和面积。

（1）r=4厘米   （2）d=4厘米

学生独立完成计算，指名两人板演。

交流：根据上面的两个条件，计算周长有什么不同？怎样想的？计算面积呢？为什么不同？

说明：条件不同，计算周长的过程就不同，计算面积也不一样，所有计算是要看清条件，根据半径、直径和周长，面积之间的关系，思考计算方法，正确列式解答。

3.分别计算下列各圆的直径和半径。

（1）C=6.28m    （2）C=15.57cm

指名学生口答列式、教师板书，要求说说怎样想的。

4.计算周长是18.84厘米的圆的面积。

提问：根据条件，求面积要先算什么，再怎样算面积？

学生独立计算，指名板演。

交流：半径是怎样求的？面积计算对不对？

追问：已知圆的周长怎样计算它的面积？

说明：计算面积一般需要知道半径，所以已知周长时，根据相互间的关系可以看出应该先算出半径，再计算面积。

三、综合练习

1、做练习十五第10题。

学生独立计算、填表。

交流填表数据，呈现表格结果。

交流：第一小题是按怎样的顺序计算的？第二小题呢？

指出：圆的计算，主要是掌握圆的各部分之间的关系，根据相互间的联系有条理地分析，找出解决问题的思路，正确解答。

2做练习十五第13题。

让学生估计三种鲜花种植面积各占花圃的几分之几，明确牡丹大约占½，玫瑰、百合大约各占¼。

学生计算面积，求出三种鲜花面积各占多少平方米。

交流结果，明确先求面积，再求出各部分面积。

3.做练习十五第14题。

引导：3个正方形中涂色部分是不是相等？同桌先讨论，互相说一说你的想法。

交流：3个正方形中涂色部分面积相等吗？为什么？

说明：我们可以通过平移、旋转的方法，或者剪拼的方法，把它们转化成相同的图形，每个图形的涂色部分都是从正方形中去掉一个圆，所有面积是相等的，

4、做练习十五第15题。

提问学生条件和问题。

让学生独立解答、指名板演。

交流：这里是按怎样的思路解答的？检查过程，看结果对不对。

还有什么解答方法？（板书算式）

说明：求小路占地面积，就是求圆环形的面积，可以用外圆面积减内圆面积解答，也可以用外圆半径平方减内圆半径平方的差乘π解答。

5、下面问题可以怎样解答？

出示：如图1是把木板（空白部分）镶嵌在大理石中间而成的圆形桌面，如果圆桌的直径是1米，那么其中大理石部分的面积是多少平方米？

提问：你想到可以怎样计算大理石部分的面积？

 

 

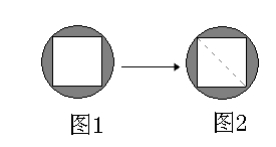
那你有办法计算正方形面积吗？【根据学生思考、交流，了解可以分成两个三角形计算正方形面积，教师在正方形内画出圆的直径（见图2），也就是正方形的对角线，让学生明确；三角形的底是直径，高是半径。】

学生解答，指名板演

检查讲评，理解其中正方形面积的计算方法。

6、完成思考题。

学生读题，思考怎样解决。

交流：黄色部分的面积可以怎样求？

先算圆的面积，圆的面积怎样计算呢？

通过交流明确：正方形面积8平方厘米，就是r²=8平方厘米，可以先求出圆面积，再求出它的¾是多少平方厘米。

四、练习总结

1.总结交流

这节课，你有哪些收获？有了哪些新的认识和体会？

2.布置作业。

完成练习十五第11、12题。

 

 

 

 

【板书设计】：

   ×2            ×π

r             d              c

 

     ÷2            ÷π

           S=πr