解决问题的策略(练习)  

 【教学内容】第3l～32页练习五第6～9题，思考题，“你知道吗”。

 【教学目标】

1、使学生在解决实际问题的过程中能根据具体问题灵活选择策略分析数量关系，确定解题思路，并正确地解决问题。

  2、使学生在应用策略解决实际问题和回顾反思中，进一步了解策略的特点和相应的解决方法、过程，发展分析和推理等思维能力。

  3、使学生进一步积累解决问题的经验，增强解决问题的策略意识，获得解决问题的成功体验，提高学好数学的信心。

4、在运用策略解决问题的过程中，能够进行合理的推理和分析。比如在假设法解决问题时，能依据假设后的结果与实际情况的差异进行逻辑推导，得出正确答案。

 【教学重点】用不同策略分析并解决实际问题。

 【教学难点】根据具体问题灵活选择策略。

【教学准备】多媒体

【教学过程】

一、谈话导入。

   1、回忆： 前两节课我们学习了解决问题的策略。回想一下，我们主要应用哪些策略来解决实际问题?（画图、转化、列举和先假设再调整等策略）。

   2、 导人：这节课我们要对这些策略进行练习。(板书课题)通过练习，同学们要能根据问题灵活选择和应用策略，解决一些实际问题。

 二、基本练习。

 1、做练习五第6题。

 （1）学生读题后交流题中的信息，说说5：6：4表示什么意思。

  (2) 提问：你能画图表示出题意吗?先试着画一画，再解答。

  (3) 学生尝试画图并解答。

  (4)集体交流，并说说是怎样想的。

 （5）规范画图，要标明条件和问题，完整解答，板书解答过程。

 （6） 小结：应用画图的策略，可以用示意图直观、清楚地表示题里数量之间的联系，方便我们分析数量关系。比如这道题通过画图，从图上能看出，上层5份共有100本，可以知道每份20本，这样就很容易得出中层和下层各有多少本；或者根据图上表示的份数和已知本数，将上层本数看成单位“1”，把中层和下层本数分别转化成是上层的和，用乘法算出各放了多少本。

2、做练习五第7题。

（1） 指名读题，理解题意。

（2） 提问：根据“货车的速度是客车的”能想到什么?（货车和客车的速度比是2:3，相遇时,货车和客车的路程比是2:3；客车行了全程的，货车行了全程的；货车路程是客车的）

(3)学生先画图再解答。（图画在书上）

（4）全班交流、讨论不同解法，板书解答过程，并比较哪种解答方法更方便一些。

（5）小结：应用画图的策略，可以清楚看出图里表示的数量关系，方便找到不同的解题方法。从图上可以看出，题里速度间的关系可以转化成货车与客车行驶的路程比是2：3，或者客车行了全程的，货车行了全程的。所以可以按比例分配解答，也可以用分数乘法计算，还可以根据货车路程是客车的，用方程解答。通过比较发现，用分数乘法算比较方便。

三、重点练习。

1、做练习五第8题。

 （1）学生读题后说说题中的信息。

（2）提问：图中第一堆的白子和黑子是怎样表示的?为什么这样表示?

    （根据“第一堆有1/3是白子”，可以把60枚棋子平均分成3份，白子有这样的1份，黑子有这样的2份。）

 （3）追问：那第二、三堆的白子和黑子可以怎样表示?再与同桌交流。

 （4）学生尝试在图中试着画一画，后交流。

 （5）学生独立列式解答后交流。

 （6）指出：根据“第二堆的黑子与第三堆的白子同样多”，从图中看：第二堆的白子和第三堆的白子合起来正好是60枚。所以先求第一堆的白子：60×＝20(枚)，第二、三堆的白子有60枚，所以这三堆棋子中一共有白子60+20＝80(枚)。

2、做练习五第9题.

  (1)学生读题，理解题意。

 （2）让学生先假设两种球分别投中的个数，再通过调整找出答案。

 （3）集体交流，并呈现假设、调整的表格，让学生说说思考的过程。

  (4)追问：你能列算式解答吗?（学生列式解答。）

 （5） 交流：你是怎样解答的?每一步表示什么意思?

     说明：列式解答时，可以先看作全部同一种分值的球，求出总分，再根据每种球相差1分，列式计算出各投中多少个。

四、拓展练习。

1、做思考题。

（1）学生读题后说说题中的信息。

    明确：单打是每张乒乓球桌2人比赛，双打是每张乒乓球桌4人比赛。

（2）提问：你准备用什么策略解决这个问题?

（3）学生独立完成，再在小组里交流你的方法。

（4）集体反馈，展示学生的不同解法。    。

(5)小结：这道题可以先假设进行单打和双打比赛乒乓球桌各有几张，再通过试验调整找出答案。例如可以先假设单打和双打比赛乒乓球桌各有6张，则单打的有6×2＝12(人)，双打的有6×4＝24(人)，通过调整，单打的有7×2＝14(人)，双打的有5×4＝20(人)，这时双打的正好比单打的多6人。

2、阅读“你知道吗”。

    谈话：同学们听说过“鸡兔同笼”的问题吗?请阅读课本第32页下面的“你知道吗”有关内容。

    学生独立阅读，并说说“今有鸡兔同笼，上有三十五头，下有九十四足，问鸡兔各几何”的意思。

学生尝试选择策略解决问题。

集体交流，让学生说出选择的策略和思考的过程。

指出：这题可以先假设鸡、兔分别有几只，再通过试验调整找出答案。

提问：这个问题可以用哪些策略解决？用画图的策略怎样解决？列举和假设的策略呢？

    引导：你能算出这道题中鸡和兔各有多少只吗？请大家用列式计算的方法求出结果．

学生独立解答后指名介绍方法、过程，教师板书算式．

追问：算式中的每一步求的是什么？

五、全课总结。

  提问：通过这节课的练习，你有哪些收获？还有什么不懂的问题吗？

  小结：在解决一些实际问题时，要根据具体问题灵活选择策略，例如应用画图、列举、假设等策略，可以更清楚地了解数量之间的关系，或者方便分析复杂问题数量之间的联系，便于找到正确的解题思路和方法，得出问题结果。

【板书设计】            解决问题的策略练习  

转化:

 

 

 

 

 

 

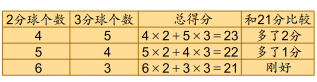
假设: （1）

    

          答：他投中2分球6个，3分球3个。

       （2） 假设全投中2分球。

           （21-2×9）÷（3—2）

          =3÷1

          =3（个）

           9-3=6(个)

        答：他投中2分球6个，3分球3个。