乘法分配律是苏教版小学数学四年级下册的内容。一直以来都是运算律教学中的一个难点，因其运算符号、运算顺序、运算数据的复杂，且极易与其他运算律相混淆，学生一下子很难理解其本质，由此导致的机械地应用模型，甚至错用模型的现象比比皆是。本文将就“乘法分配律”一课为例，谈谈小学阶段规则教学中应如何充分经历探究过程，借助几何直观来实现有效建模。

《义务教育数学课程标准（2022 年版）》指出：几何直观建立形与数的联系，构建数学问题的直观模型；有助于把握问题的本质，明晰思维的路径。小学阶段运算律的教学，基本都是先从孩子们熟悉的生活情境中抽象出数学问题，然后用举例验证的方法理解、讨论这些式子的意义并得出结论，最后用含有字母的式子表示运算中的变化规律，这就是小学阶段运算律教学环节学生建立几何直观和应用模型的过程。 在四年级《乘法分配律》一课的教学设计中，我设计了“提出猜想——举例验证——得出结论——解释说理——巩固应用”的教学步骤，让学生有贴近生活的教学素材，有独立举例的验证环节，有数形结合的解释说理，最终在学生头脑中构建起“乘法分配律”的数学模型。

片断一：借助现实情境，提出数学问题

师：同学们,今天老师把超市散装零售区十几种口味的薯片都带到了教室。可是超市服务台的阿姨说像我这样分十几个袋子分开买太麻烦了，如果这些不同口味的薯片放在一个袋子里来称重计费就会方便许多。既然这么多薯片能放在一起称重，那么再加些你们喜欢的巧克力、奶糖、饼干应该也可以吧。可服务台的阿姨却皱起了眉头，把这些东西一股脑倒了出来，分别装在几个口袋中来称重计费。这下我可犯迷糊了，有谁能告诉告诉老师这是为什么吗？

生₁：我知道，不同口味的薯片，单价肯定是一样的，所以就是放在一起称；而后来的巧克力、奶糖、饼干单价肯定有好几种，所以只能分开称。

生₂：散称食品的计费方法是单价×重量=总价，所以只要单价相同就可以放在一起称重并算出总价。

生₃：其实不同口味的薯片也可以分开称，先称出每种薯片的重量，再乘薯片的单价，就能算出这一口味薯片的总价；再把每种薯片的总价相加，就能知道所有口味薯片的总价。如果放在一起称，就是把每种口味薯片的重量也相加，再去乘薯片的单价，也能算出所有口味薯片的总价。

生₄:我觉得薯片还是放在一起称比较好，这样既能节约塑料袋保护环境，也能方便计算总价，只要进行一次乘法运算就可以了。

师：同学们，看来大家的生活经验、数学知识、环保理念都很棒哦。既然购物中藏着这么有趣的数学问题，今天我们就一起来研究吧。

【思考】：众所周知，情境的创设要充分关注学生现有的认知水平和生活经验，所选择的素材要尽可能贴近学生的实际生活，这样才会更容易让孩子们从现实情境中抽象出数学问题。所以本课情境导入的设计没有直接使用书本的例题，而是先播放了一段从学生熟悉的超市购物场景：不同的散称商品有时可以放在一起称重计费，有时却不可以，这到底是为什么呢？这样贴近生活的问题情境，很可能是孩子们在以前购物中已经遇到过并产生疑问的。超市的工作人员或孩子的父母极有可能已经帮助其答疑解惑过，这一点从孩子们的回答中也可以看出来，大部分学生其实都已经发现只要散称商品的单价相同，就有两种不同的解决方法。贴近生活的问题情境充分激发了学生解决问题的欲望，同时也能唤醒他们已有的学习经验,由孩子们自己提出想要解决的问题，并进一步引导到本课“乘法分配律”的例题教学。一段对话沟通了外部世界与数学课本的联系，让学生由解决问题者转变为问题创造者，充分体现了生本数学的魅力。

片断二：充分举例验证，初步建构模型

师：出示例5题图，让两种不同方法解答的学生说一说并板书。

生₁：（6+4）×24

生₂：6×24+4×24

追问：（6+4）×24这种方法是先求了什么，再求了什么的？6×24+4×24这种方法呢？

生₁：（6+4）×24先求了四、五年级一共有几个班，再求了四、五年级一共要领多少根跳绳。

生₂：6×24+4×24先分别求出了四、五年级各要领多少根跳绳，再求出了四、五年级一共要领多少根跳绳。

师：比较最后的计算结果，你有什么发现吗？

齐：两种方法结果相等。

师：这两个算式虽然不一样，但他们都在解决同一个问题，结果也相同，我们可以在两个算式之间画上等号。

板书：（6+4）×24=6×24+4×24

提问：观察等号两边的算式，想一想，它们之间有什么联系？

生：左边先算了6+4的和，再去和24相乘，右边先算6×24和4×24的积，再相加。

追问：计算时，等号的左右两边有怎样的结构变化呢？等号两边的数有什么联系吗？用手势表示出左右之间的联系。

生：6和4可以合起来乘24，也可以分开来乘24。

师：大家可以试着补充两个同类型的式子并计算答案，看看等式两边的结果是否相等？

师：因为他们有相同的乘数，我们可以合起来乘相同的乘数，也可以分开来乘相同的乘数。同学们，刚才我们对黑板上的这几个等式进行了观察比较，提出了一个想法，这只是我们的一个猜想。这个猜想到底对不对呢，我们需要怎么做？

生：可以举例看看。

师：好的，那我们每人写出两组这样的算式，先分别算出得数，如果得数相等的话用等号连接。

在独立举例验证环节，指名一些同学到黑板上板演。

提问：观察黑板上的每一个等式，说说它们有什么共同的特点？这样的等式写得完吗？你们写出的这样一组算式有没有不相等的？

师：我们能举出很多这样两边相等的式子，一个反例也没有找到，看来刚才咱们的猜想是正确的。现在能不能用一句话把你们的发现总结出来。

生：两个数的和与一个数相乘，可以先把这两个数分别与这个数相乘，再相加。（教师板书）

师：我觉得用语言表达还是比较麻烦，有没有更好的方法呢？

生板书：（a+b）×c=a×c+b×c

师：这就是我们今天要认识的运算律新朋友——乘法分配律，用字母表示就是（a+b）×c=a×c+b×c。

【思考】：在小学阶段运算律的教学中，观察比较、举例验证可以说是无处不在。课始学生已经结合生活素材中提出了数学问题，此处走进书本在例题教学中让两种不同方法解答的同学观察比较两个算式之间的联系，并充分举例验证。让每个同学写出两组这样的算式并计算比较，适时指名了一些同学进行板书。板书时教师让学生先对每道等式进行横向观察比较，虽然等式左右两边的结构不一样，但都有一些相同的数字；再对多道算式进行纵向观察比较，发现这些等式左边都是两个数先相加，再和第三个数相乘的算式；右边都是两个数先分别与第三个数相乘，再把乘得的积相加的算式；最后进一步追问是否可以举出反例。虽然这样的观察比较、举例验证还只是不完全归纳，学生认知上对乘法分配律的数学模型还是比较浅显模糊的，但已经在学生脑海中初步建构起了乘法分配律的数学模型。

片断三：严谨探究本质，内化提升模型

师：为什么会有这样的规律呢？其中又有怎样的道理呢？我们来看这样一个算式：（4＋5）×3= 4×3＋5×3，谁来说一下这个乘法算式的意义。

生₁： 4+5个3等于4个3加5个3。

生₂： 我觉得也可以看成3个4+5的和。

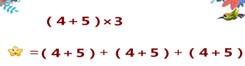PPT相机出示算式：

师：看了这个加法算式，你们有什么想法：

生：可以调整加数的位置，把加数4放在一个括号里，把加数5放在另一个括号里？

PPT动态演示，调整加数的位置。

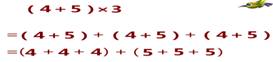师:通过调整加数的位置，4+4+4可以用乘法4×3表示，5+5+5可以用乘法5×3表示。应用乘法的意义，我们证明了（4＋5）×3= 4×3＋5×3。

师：刚才我们用举例验证的方法证实了咱们的猜想，得到了乘法分配律的字母表达式为（a+b）×c=a×c+b×c。

数学是一门非常严谨的学科，除了举例验证外，我们还需要用严谨的方法来对乘法分配律再次进行验证。能不能仿照（4＋5）×3的验证方法，来对乘法分配律进行验证呢？

PPT动态演示乘法分配律意义的严谨推理：

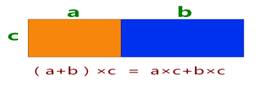
师：刚才是用乘法的意义对乘法分配律进行了验证，接下来我们用更为直观的方法来验证。

生：我知道，橙色长方形的面积可以用a×c来表示，蓝色长方形的面积可以用b×c来表示，大长方形的面积可以用（a+b）×c来表示。从图中我们可以看出，大长方形的面积等于橙色和蓝色两个长方形面积之和，所以（a+b）×c=a×c+b×c。

【思考】：探究乘法分配律这一数学知识的本质是本课教学的核心。以往的教学中，我们在从正反两个方向举例验证初步建构模型的基础上，就让学生直接进入练习环节习得经验，并直觉认为学生已经充分理解并掌握乘法分配律了。本课的设计中，我把重点放在了通过理解乘法的意义去掌握算理和算法。

一是化静为动，让学生明白乘法的意义是乘法分配律知识的起点，其本质是对几个相同加数的分与合。字母表达式（a+b）×c=a×c+b×c的顺向意义是：（a+b）个c的和分为a个c与b个c的和；逆向意义是：a个c与b个c的和合为（a+b）个c的和。这样从左到右（或从右到左）的推导过程，是学生在教师的指导下运用已有知识独立探究的结构特点，并在此过程中进一步完善了数学模型。

二是数形结合，加深理解。“数无形时少直觉，形少数时难入微”，教学中，运用数形结合是一种行之有效的教学策略。教学“乘法分配律”时，要充分利用“数形结合”的教学思想与策略，通过“式”与“形”的一一对应，以及做实做厚规则教学的建模过程，真正实现有效建模的目的。在本课例中首先准备了两个宽相等的长方形，橙色长方形长a、宽c，蓝色长方形长b、宽c，这一直观模型可以先分别求出两个长方形的面积，然后沿宽拼接在一起，成为一个边长为a+b的大长方形，再算出大长方形的面积。在直观图形面积计算中，从学生已有的知识经验出发，把教学落到学生的难处和需要处，才能真正走进学生的思维世界，从而使学生深入理解数学模型。

片断四：借助几何直观，拓展衍生模型

1.在□里填数，在○里填运算符号。

(1)（42+35）×2=42×□+35×□

(2)27×12＋43×12＝（27＋□）×□

(3)15×26+15×14=□○（□○□ ）

(4)72×(30+6) = □○□○□○□

师：谁能说一说第（2）题你是怎么想的？

生：这题要求的是两积之和，我发现算式中有相同的乘数12，这个相同的乘数可以放在括号外面。

师：非常棒。让我们从算式的右边往左看，是不是刚才咱们学习的乘法分配律，这就是乘法分配律的逆向应用。

2、

师：刚才我们看图知道了大长方形的面积等于拼成的两个小长方形面积的和。如果我想知道这两个小长方形的面积差，你能帮忙算一算吗？

生₁：橙色长方形的面积可以用a×c来表示，蓝色长方形的面积可以用b×c来表示，从图中可以看出蓝色长方形面积大一些，所以面积差就是b×c-a×c。

生₂：我觉得刚才的题中并没有告诉我们a和b哪一条边更长一些，这时候我们可以把两个长方形重叠起来比一比，多出来那一块就是面积差。

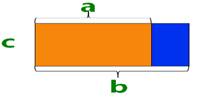师：蓝橙两个长方形的面积差，也就是你刚才说的多出来的那一块是什么形状，你会计算出它的面积吗？

生₂：这是一个小长方形，其中一条边是b-a，另一条边是c，所以面积就是（b-a）×c。

师：的确如此，从图中我们可以看出，蓝色和橙色两个长方形面积之差等于它们重叠后多出来的那个小长方形的面积，所以（a-b）×c=a×c+b×c。

【思考】每个学生的学习潜能是存在差异的，如果本课教学仅停留在让学生概括出并理解(a+b)×c=a×c+b×c显然对于学有余力的同学来说是远远不够的。于是我先是结合练一练“27×12＋43×12＝（27＋□）×□”一题，引导学生先在两积之和中找到相同的乘数12，把它放到括号的外面；再带着学生从右到左进行观察，让学生初步接触乘法分配律的逆向应用。

为了满足不同的学生的学习需要，借助前面的橙色、蓝色长方形图继续追问面积差，引发学生对“乘法对减法的分配规律”的思考这一问题。这一问题的提出让“乘法对加法的分配规律”这一基本的数学模型再次“发芽生长”。孩子们的回答比预想的更为出彩，将图形重叠、比较，得出面积差也可以用（a-b）×c来表示。学生的浅层学习已自觉转为深度学习，在数形结合中进一步加深了对乘法分配律内涵的认识，也激发了学生深入探索乘法分配律模型适用的范围，为乘法分配律在实际中的灵活运用打下坚实的基础。

总之，就本课教学而言，我们一直在尝试充分经历每一段过程，从而更好构建乘法分配律的数学模型。本课数学建模的过程，我们经历了“提出猜想——举例验证——得出结论——解释说理——巩固应用”这五个环节，学生们充分调动原有知识和经验去尝试解决自己根据超市购物情境提出的新问题，在举例验证和严谨推导中，同化新知识并建构出数学模型。其实小学阶段各项运算律的教学都可以通过建模形成数学模型，让学生知其然更知其所以然，进而对数学产生更大的兴趣，逐步提升学生的综合素养。

【参考文献】

1.中华人民共和国教育部.义务教育数学课程标准（2011年版）［M］.北京：北京师范大学出版社，2012.

2.“情智共生，趣效双赢”教学风格的形成与思考——以执教“乘法分配律”一课为例 [J]. 丁玉华.数学教学通讯.2020(04)