

加入时间:2022-05-25

加入时间:2022-06-21

加入时间:2022-05-25

加入时间:2022-05-25

加入时间:2022-05-25

加入时间:2022-05-25

加入时间:2022-05-25
加入时间:2022-05-25

加入时间:2022-05-25

加入时间:2022-05-25

加入时间:2022-05-25

加入时间:2022-05-25

加入时间:2022-05-25

加入时间:2022-05-25
加入时间:2022-05-25

加入时间:2022-05-25
加入时间:2022-05-25

加入时间:2022-05-25
教 案(首页)
编号:YJSD/JWC-17-08
|
课题序号 |
27 |
授课班级 |
联五24建筑智能 |
|
授课课时 |
2 |
授课形式 |
新授课 |
|
授课章节 名称 |
§5.2 弧度制 |
||
|
使用教具 |
无 |
||
|
教学目的 |
(1)使学生理解弧度制的意义,能正确地进行弧度与角度的换算,熟记特殊 角的弧度数; (2)了解角的集合与实数集R之间可以建立一一对应的关系; (3)掌握弧度制下的弧长及扇形面积计算公式,会用弧度制解决一些实际问题。 |
||
|
教学重点 |
角度和弧度的转化 |
||
|
教学难点 |
对度量角的弧度制的理解 |
||
|
更新、补 充、删减 内容 |
无 |
||
|
课外作业 |
课后习题P151 |
||
|
教学后记 |
学生对于角度和弧度的转化较熟练,但对于用弧度制表示终边相同的角有困难。 |
||
|
授课主要内容或板书设计 |
|||
|
§5.2 弧度制 一、弧度制的定义 例题 学生练习
二、弧度与角度的互化
三、用弧度制表示终边相同的角
四、弧长公式和扇形面积公式 |
|||
§ 5.2 弧度制
[学习任务]
1、能力目标:发展学生应用数学知识与方法解决问题的意识和能力,让学生从中体会数学的价值。
2、知识目标:
(1)使学生理解弧度制的意义,能正确地进行弧度与角度的换算,熟记特殊角的弧度数;
(2)了解角的集合与实数集R之间可以建立一一对应的关系;
(3)掌握弧度制下的弧长及扇形面积计算公式,会利用弧度制解决一些简单的实际问题。
3、情感目标:激发学生的非智力因素,增强学生学习数学的兴趣,强化学生积极参与的主体
意识。
[重点和难点]
重点:角度和弧度的转化
难点:对度量角的弧度制的理解
[教学模式与方法] 情境问题导向式教学模式
[学习活动] 师生互动
[主要知识点]
1、弧度制的定义:___________________________________叫1弧度的角,记作1(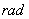 )
)
2、弧度与角度的互化:
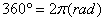
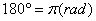


特殊角的度数与弧度数的转化:
|
角度 |
|
|
|
|
|
|
|
|
|
|
|
|
弧度 |
|
|
|
|
|
|
|
|
|
|
|
3、用弧度制表示终边相同的角:
与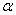 角终边相同的角的集合:______________________________
角终边相同的角的集合:______________________________
4、弧长公式和扇形面积公式:
已知角的顶点在圆心,圆的半径为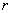 ,用弧度制表示角的大小为
,用弧度制表示角的大小为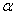 ,这个角所对的圆弧的长度为
,这个角所对的圆弧的长度为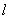 。
。
弧长公式为: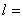 __________________
__________________
扇形面积公式为: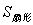 =_______________________
=_______________________
刻画物体的质量、长度、体积、温度、速度等时,度量单位一般是借助工具制定的.比如,中国人所说的“拃”就是古代中国的“尺”,指的是成年男人大拇指与中指之间的距离,在西方的许多国家仍然把“英尺”(foot)作为度量单位,英文单词foot是脚的意思,指的是成年男子一只脚的长度.这样制定的长度单位是因人因地而异的,是无法进行传播和交流的,因此长度单位的制定需要从多元走向统一.现在统一使用的国际基本长度单位是“米”,这样的度量依赖的是人对距离远近的感知本能.在不同的情况下,人们使用不同的度量单位,例如,在衡量天体之间的距离时用“光年”作为单位,而在衡量芯片制程时用“纳米”作为单位.
初中我们学过用“度”作单位度量角的单位制称为角度制.还可采用什么作单位度量角呢?
如图5-8,两个半径为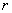 与
与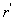 的同心圆如果圆心角
的同心圆如果圆心角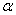 的大小是确定的.
的大小是确定的.
(1)在不同的圆中,同样的圆心角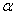 所对的弧长
所对的弧长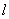 与
与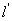 是否相等?
是否相等?
(2)在不同的圆中,同样的圆心角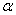 所对应的弧长与半径的比值是否相等?其比值大小与半径有关还是由圆心角大小确定?
所对应的弧长与半径的比值是否相等?其比值大小与半径有关还是由圆心角大小确定?
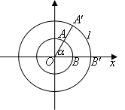 |
图5-8
对问题(1),我们知道,在圆周中,弧长所占圆的周长的份数等于该弧所对圆心角所占圆周角的份数,根据角度制得,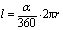 ,
,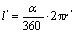 所以,当半径不相等时,同样的圆心角所对的弧长不相等;
所以,当半径不相等时,同样的圆心角所对的弧长不相等;
对问题(2),根据对问题(1)的分析得,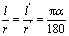 ,即同样的圆心角
,即同样的圆心角 所对应的弧长与半径的比值相等.并且弧长与半径的比值与半径无关,是由圆心角的大小确定的.由此可见,圆心角所对应的弧长与半径的比值大小,能刻画圆心角的大小.
所对应的弧长与半径的比值相等.并且弧长与半径的比值与半径无关,是由圆心角的大小确定的.由此可见,圆心角所对应的弧长与半径的比值大小,能刻画圆心角的大小.
二、抽象概括
如果圆心角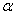 的大小确定,则圆心角
的大小确定,则圆心角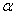 所对应的弧长与半径的比值是一个常数,我们称这个常数为圆心角
所对应的弧长与半径的比值是一个常数,我们称这个常数为圆心角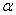 的弧度数.当圆的半径为1个单位长度时,圆心角
的弧度数.当圆的半径为1个单位长度时,圆心角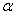 所对的弧长就是这个角的弧度数.
所对的弧长就是这个角的弧度数.
长度等于半径的弧所对的圆心角叫做1弧度的角,记此角为1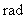 (读作1弧度).
(读作1弧度).
三、合作交流
弧长等于2倍半径的弧所对的圆心角弧度数是多少?直角的弧度数是多少?
由于平角的弧度是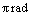 ,并且角度制下1个平角为
,并且角度制下1个平角为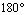 ,所以
,所以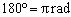 .
.
由此可得到角度与弧度的换算关系:
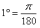 rad
rad 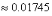
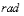 , 1
, 1 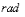 =
= 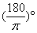
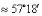
规定:正角的弧度数为正数,负角的弧度数为负数,零角的弧度数为0.当形成角的射线旋转一周后继续旋转,就可以得到弧度数大于2π或小于-2π的角,这样,就可用角的弧度数度量任意角的大小.并建立了角的集合与实数集R之间一一对应的关系.用弧度作单位(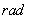 常省略不写)来度量角的单位制叫做弧度制.
常省略不写)来度量角的单位制叫做弧度制.
四、例题解析
例1 把45°化成弧度.
例2 把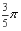
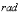 化成度.
化成度.
例3 将下列各角化成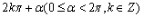 的形式,并指出是第几象限角?
的形式,并指出是第几象限角?
(1)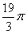 ; (2)
; (2)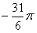 .
.
五、思维拓展
用弧度制如何表示轴线角、象限角的集合.
(1)终边落在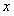 轴的非正、非负半轴,
轴的非正、非负半轴,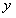 轴的非正、非负半轴的角.
轴的非正、非负半轴的角.
(2)第一、二、三、四象限角.
六、课内练习
1.将下列各角化为弧度:
(1)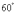 ;(2)
;(2) 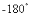 ;(3)
;(3)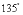 ;(4)
;(4) 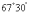 .
.
2.将下列各角化为角度:
(1)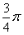 ;(2)
;(2)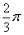 ;(3)
;(3) ;(4)
;(4) .
.
七、课堂小结
1.了解1弧度的定义及弧度制;
2.掌握角度制与弧度制的互化;
3.熟记特殊角的弧度数.
在初中已经学习了角度制下计算弧长的公式及计算扇形面积的公式.如图5-9,圆的半径是r,圆心角为α度,则弧长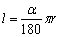 ,以α为圆心角的扇形面积
,以α为圆心角的扇形面积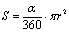 .
.
那么,在弧度制下,弧长与扇形面积公式又是怎样的呢?
如图5-9,圆的半径是r,圆心角α的单位是弧度,那么,如何用r, α表示圆心角α所对的弧长l及扇形面积S?
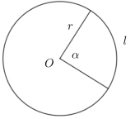
图5-9
二、抽象概括
如图5-9,由弧度的定义,弧长l与半径r的比值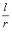 等于所对圆心角α的弧度数,又α有正负由α的始边到终边的旋转方向确定,所以,
等于所对圆心角α的弧度数,又α有正负由α的始边到终边的旋转方向确定,所以,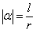 (其中
(其中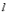 表示
表示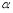 所对的弧长),即
所对的弧长),即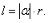
这就表明弧长等于该扇形圆心角的弧度数的绝对值与半径之积.
又因为:在圆周中,扇形所占圆的面积的份数等于该扇形所在圆心角所占圆周角的份数,所以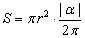 .
.
因此,扇形面积公式为: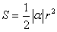
由于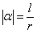 ,所以扇形面积公式还可用α和r表示为
,所以扇形面积公式还可用α和r表示为 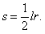 .
.
即扇形面积等于扇形的弧长与半径之积的一半.
三、例题解析
例4 在半径为5cm的扇形中,圆心角为4rad,求扇形的面积.
例5 扇形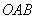 的面积是
的面积是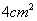 ,它的周长是
,它的周长是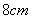 ,求扇形的圆心角.(如图5-10)
,求扇形的圆心角.(如图5-10)
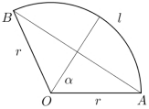
图5-10
四、思维拓展
已知公路上一段圆弧形弯道半径是30m,转过的圆心角是120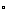 ,该弯道的长度是多少?
,该弯道的长度是多少?
五、课内练习
1.直径为20cm的滑轮,每秒钟旋转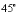 ,则滑轮上一点经过5秒钟转过的弧长是多少?
,则滑轮上一点经过5秒钟转过的弧长是多少?
2.在半径为12cm的扇形中,圆心角为4rad,求该扇形的弧长和面积.
六、课堂小结
1.终边相同角的概念;
2.终边相同角的表示法.