

加入时间:2022-05-25

加入时间:2022-06-21

加入时间:2022-05-25

加入时间:2022-05-25

加入时间:2022-05-25

加入时间:2022-05-25

加入时间:2022-05-25
加入时间:2022-05-25

加入时间:2022-05-25

加入时间:2022-05-25

加入时间:2022-05-25

加入时间:2022-05-25

加入时间:2022-05-25

加入时间:2022-05-25
加入时间:2022-05-25

加入时间:2022-05-25
加入时间:2022-05-25

加入时间:2022-05-25
教 案(首页)
编号:YJSD/JWC-17-08
|
课题序号 |
3 |
授课班级 |
联五24工程技术 |
|
授课课时 |
2 |
授课形式 |
新授课 |
|
授课章节 名称 |
§1.3 集合的运算 |
||
|
使用教具 |
多媒体 |
||
|
教学目的 |
(1)理解两个集合的并集与交集的含义,会求两个简单集合的并集与交集; (2)了解给定集合中的一个子集的补集的意义,并会求给定子集的补集; (3)能用维恩图表达集合的关系,并能体会直观图示对理解抽象概念的作用.
|
||
|
教学重点 |
理解两个集合的交集、并集,了解全集、补集的含义; |
||
|
教学难点 |
在理解两个集合的交集、并集,了解全集、补集的含义的基础上,会结合维恩图进行集合的运算. |
||
|
更新、补 充、删减 内容 |
无 |
||
|
课外作业 |
课后习题P19 |
||
|
教学后记 |
学生能够两个集合的并集与交集的含义,会求两个简单集合的并集与交集,并会求给定子集的补集。 |
||
|
授课主要内容或板书设计 |
|||
|
§1.3 集合的运算 一、交集 二、并集 三、补集
例题 例题 例题
|
|||
§1.3 集合的运算
[学习任务]
1、知识与能力目标:
(1)理解两个集合的并集与交集的含义,会求两个集合的交集与并集;
(2)了解补集的含义,会求给定子集的补集。
2、过程与方法目标:让学生初步感受数学建模思想,能够利用数形结合分析和解决相关问题。
3、情感态度与价值观目标:提高学生的实际应用能力,真正体会到学习的乐趣,感受到学有所得,学有所用。
[重点和难点] 正确地进行集合之间的交、并、补运算
[教学模式与方法] 情境问题导向式教学模式
[学习活动] 师生互动
[主要知识点]
一、交集
1、 定义:一般地,给定两个集合A,B,由____________________的元素组成的集合,叫做集合A与集合B的交集,记作___________,即________________________________。
2、 图示:
3、
性质⑴A∩A=________
A∩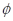 = _______
= _______
⑵A∩B______ A A∩B_____ B
⑶若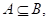 则
则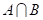 =_______
=_______
⑷A∩B ____B∩A (A∩B)∩C_____A∩(B∩C)
二、并集
1、定义:一般地,给定两个集合A,B,把它们所有的元素_______________组成的集合,叫做集合A与集合B的并集,记作___________,即________________________________。
2、图示:
3、性质⑴A∪A=________
A∪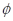 = _______
= _______
⑵A______ A∪B B_____ A∪B
⑶若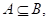 则
则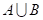 =_______
=_______
⑷A∪B ____B∪A (A∪B)∪C_____A∪(B∪C)
三、补集
1、定义:一般地,如果我们所研究的集合涉及的全部元素都________集合U,那么集合U叫做全集。如果A是全集U的一个_________,由U中___________A的所有元素组成的集合叫做集合A在全集U中的补集,记作__________,即___________________________。
2、性质:(1)__________________
(2)__________________
(3)__________________
1.3.1 并集
一、问题探究
考察下面两组集合,集合C的元素与集合A、B之间具有怎样的关系?
(1) ={1,2,3},
={1,2,3}, ={2,3,4},
={2,3,4},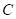 ={1,2,3,4};
={1,2,3,4};
(2) ={x|x=2k,k∈Z},
={x|x=2k,k∈Z}, ={x|x=2k+1,k∈Z},
={x|x=2k+1,k∈Z},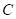 =Z.
=Z.
容易看出,在上述两组集合中,集合C是由所有属于集合A或属于集合B的元素组成的.
二、抽象概括
1.并集与并运算
一般地,由所有属于集合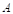 或属于集合
或属于集合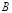 的元素组成的集合称为集合
的元素组成的集合称为集合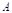 与集合
与集合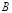 的并集,记作
的并集,记作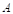 ∪
∪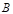 ,读作“
,读作“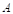 并
并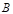 ”,即
”,即
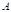 ∪
∪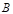 ={x|x∈
={x|x∈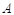 或x∈
或x∈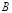 }.
}.
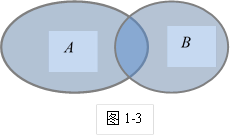
 ∪
∪ 可以用图1-3中的阴影部分来表示.
可以用图1-3中的阴影部分来表示.
并集 ∪
∪ 是由给定的两个集合
是由给定的两个集合 、
、 通过“将两个集合的所有元素合并到一起”这样的“运算”得到的新集合.这种运算称为“并” .
通过“将两个集合的所有元素合并到一起”这样的“运算”得到的新集合.这种运算称为“并” .
2、并运算的性质
对于任意集合 ,
, ,
,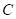 ,有
,有
(1) 交换律: ∪
∪ =
= ∪
∪ ;
;
(2) 结合律:( ∪
∪ )∪
)∪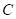 =
= ∪(
∪( ∪
∪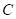 ).
).
三、例题讲析
例1 设集合 ={1,3,4,7}, 集合
={1,3,4,7}, 集合 ={2,4,6,7},求
={2,4,6,7},求 ∪
∪ .
.
解  ∪
∪ ={1,3,4,7}∪{2,4,6,7}={1,2,3,4,6,7}.
={1,3,4,7}∪{2,4,6,7}={1,2,3,4,6,7}.
例2 设集合 ={x|0<x<2},集合B={x|x≥1},求
={x|0<x<2},集合B={x|x≥1},求 ∪
∪ .
.
解 集合 、
、 可以在数轴上表示为如图1-4所示的形式,由图可知,
可以在数轴上表示为如图1-4所示的形式,由图可知,
 ∪
∪ ={x|0<x<2}∪{x|x≥1}={x|x>0}.
={x|0<x<2}∪{x|x≥1}={x|x>0}.

四、合作交流
1.如果两个集合 、
、 满足
满足
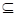
 ,那么
,那么 ∪
∪ =
.
=
.
反之成立吗?
2. ∪
∪ = ,
= ,  ∪
∪ = .
= .
五、练习
1.填空题
(1)若集合 ={-1,0,2,5},集合
={-1,0,2,5},集合 ={-2,0,2,6},则
={-2,0,2,6},则 ∪
∪ = ;
= ;
(2)若集合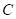 ={x|x>-1},集合
={x|x>-1},集合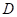 ={x|x>2},则
={x|x>2},则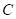 ∪
∪ =
;
=
;
(3)若集合E={x|x是三角形},集合F={x|x是直角三角形},则E∪F= ;
(4)若集合G=N,集合H=Q,G∪H= .
2.设集合 ={x|x<5},集合
={x|x<5},集合 ={x|x<-1},求
={x|x<-1},求 ∪
∪ .
.
1.3.2 交集
一、问题探究
考察下面两组集合,集合 的元素与集合
的元素与集合 、
、 之间具有怎样的关系?
之间具有怎样的关系?
(1) ={1,2,3},
={1,2,3}, ={2,3,4},
={2,3,4},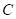 ={2,3};
={2,3};
(2) ={x|x=2k,k∈Z},
={x|x=2k,k∈Z}, ={x|x=3k,k∈Z},
={x|x=3k,k∈Z},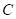 ={x|x=6k,k∈Z}.
={x|x=6k,k∈Z}.
容易看出,在上述两组集合中,集合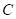 是由所有既属于集合
是由所有既属于集合 又属于集合
又属于集合 的元素组成的.
的元素组成的.
二、抽象概括
1、交集与交运算
一般地,给定两个集合 ,
, ,由既属于集合
,由既属于集合 又属于集合
又属于集合 的元素组成的集合,称为集合
的元素组成的集合,称为集合 与集合
与集合 的交集,记作
的交集,记作 ∩
∩ ,读作“
,读作“ 交
交 ”,即
”,即
 ∩
∩ ={x|x∈
={x|x∈ 且x∈
且x∈ }.
}.
 ∩
∩ 可以用图1-5中的阴影部分来表示.
可以用图1-5中的阴影部分来表示.
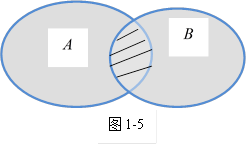 |
交集 ∩
∩ 是由给定的两个集合
是由给定的两个集合 、
、 通过“将两个集合的相同元素合并到一起”这样的“运算”得到的新集合.这种运算称为“交”.
通过“将两个集合的相同元素合并到一起”这样的“运算”得到的新集合.这种运算称为“交”.
2、交运算的性质
对于任意集合 ,
,  ,
,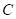 ,有
,有
(1) 交换律: ∩
∩ =
= ∩
∩ ;
;
(2) 结合律:( ∩
∩ )∩
)∩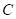 =
= ∩(
∩( ∩
∩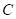 ).
).
三、例题讲析
例3 设集合 ={a,b,d,e},集合
={a,b,d,e},集合 ={b,c,e,f},求
={b,c,e,f},求 ∩
∩ .
.
解  ∩
∩ ={a,b,d,e}∩{b,c,e,f}={b,e}.
={a,b,d,e}∩{b,c,e,f}={b,e}.
例4 设集合 ={x|-2<x<2}, 集合
={x|-2<x<2}, 集合 ={x|x≥0},求
={x|x≥0},求 ∩
∩ .
.
解 集合 、
、 可以在数轴上表示为如图1-6所示的形式,由图可知,
可以在数轴上表示为如图1-6所示的形式,由图可知,
 ∩
∩ ={x|-2<x<2}∩{x|x≥0}={x|0≤x<2}.
={x|-2<x<2}∩{x|x≥0}={x|0≤x<2}.
四、合作交流
1.如果两个集合 、
、 满足
满足
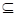
 ,那么
,那么 ∩
∩ =
.
=
.
反之成立吗?
2. ∩
∩ =
,
=
,  ∩
∩ =
.
=
.
五、练习
1.填空题
(1)若集合 ={a,b,c,d,e},集合
={a,b,c,d,e},集合 ={b,d,f},则
={b,d,f},则 ∩
∩ =
.
=
.
(2)若集合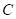 ={x|x<3},集合
={x|x<3},集合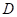 ={x|x>2},则
={x|x>2},则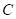 ∩
∩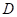 =
.
=
.
(3)若集合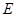 ={x|x是正方形},集合
={x|x是正方形},集合 ={x|x是矩形},则
={x|x是矩形},则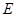 ∩
∩ =
.
=
.
(4)若集合 =Z,集合
=Z,集合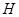 =R,则
=R,则 ∩
∩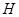 = .
= .
2. 设集合 ={x|-1<x<4},集合
={x|-1<x<4},集合 ={x|0<x<7},求
={x|0<x<7},求 ∩
∩ .
.
1.3.3 补集
一、问题探究
考察下面两组集合,集合 ,
, ,
, 之间都具有怎样的关系?
之间都具有怎样的关系?
(1) ={1,2,3},
={1,2,3}, ={4},
={4}, ={1,2,3,4};
={1,2,3,4};
(2) ={x|x=2k,k∈Z},
={x|x=2k,k∈Z}, ={x|x=2k+1,k∈Z},
={x|x=2k+1,k∈Z}, =Z.
=Z.
容易看出,在上述两组集合中,集合 、
、 都是集合
都是集合 的子集,且集合
的子集,且集合 是由集合
是由集合 中不属于
中不属于 的元素组成的,集合
的元素组成的,集合 是由集合
是由集合 中不属于
中不属于 的元素组成的.
的元素组成的.
二、抽象概括
1、全集与补集的概念
一般地,在研究某些集合时,这些集合通常是一个给定集合的子集,这个给定的集合称为全集,一般用 来表示.
来表示.
如果 是全集
是全集 的一个子集,由集合
的一个子集,由集合 中不属于
中不属于 的所有元素组成的集合称为集合
的所有元素组成的集合称为集合 在全集
在全集 中的补集,记作CU
中的补集,记作CU ,读作“
,读作“ 在
在 中的补集”,即
中的补集”,即
CU ={x|x∈
={x|x∈ ,且x
,且x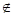
 }.
}.
CU 可以用图1-7中的阴影部分来表示.
可以用图1-7中的阴影部分来表示.

2、补运算及运算性质
补集CU 是由给定的两个集合
是由给定的两个集合 、
、 通过“将集合
通过“将集合 中不属于
中不属于 的所有元素合并到一起”这样的“运算”得到的新集合.这种运算称为“补”.
的所有元素合并到一起”这样的“运算”得到的新集合.这种运算称为“补”.
对于全集 和它的一个子集
和它的一个子集 ,有
,有
(1) ∪(CU
∪(CU )=
)= ;
;
(2)  ∩CU
∩CU =
= .
.
三、例题讲析
例5 已知全集 ={1,2,3,4,5,6},集合
={1,2,3,4,5,6},集合 ={1, 3,4},求CU
={1, 3,4},求CU .
.
解 因为全集 ={1,2,3,4,5,6},集合
={1,2,3,4,5,6},集合 ={1, 3,4},所以
={1, 3,4},所以
CU ={2,5,6}.
={2,5,6}.
例6 已知全集 =R, 集合
=R, 集合 ={x|x<1},求CU
={x|x<1},求CU .
.
解 因为全集 =R, 集合
=R, 集合 ={x|x<1},所以
={x|x<1},所以
CU ={x|x≥1}.
={x|x≥1}.
合作交流
CU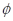 =
, CU
=
, CU =
,CU(CU
=
,CU(CU )=
.
)=
.
四、思维拓展
某班级共有28人同时参加数学和英语竞赛.经测试,其中数学有12人获奖,英语有14人获奖,有5人两科都获奖,求没有获奖的人数.
五、练习
1.填空题
(1)全集 ={a,b,c,d,e,f},集合
={a,b,c,d,e,f},集合 ={b,d,f},则CU
={b,d,f},则CU =
;
=
;
(2)全集 ={x|x是三角形},集合
={x|x是三角形},集合 ={x|x是锐角三角形},则CU
={x|x是锐角三角形},则CU =
;
=
;
(3)全集 =Z,集合
=Z,集合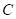 ={x|x=2k-1, k∈Z},则CU
={x|x=2k-1, k∈Z},则CU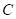 =
;
=
;
(4)全集 =R, 集合
=R, 集合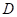 ={x|x≤2},则CU
={x|x≤2},则CU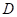 =
;
=
;
(5)全集 =R, 集合
=R, 集合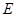 ={x|-2<x≤4},则CU
={x|-2<x≤4},则CU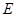 =
.
=
.
2.已知全集 =R, 集合
=R, 集合 ={x|x<2},集合
={x|x<2},集合 ={x|x>0},求
={x|x>0},求 ∪
∪ ,
,  ∩
∩ , CU
, CU ,CU
,CU .
.
六、课堂小结
1.交集的概念及符号
2.理解“且”的含义
3 .学会借助“数轴”解决问题的方法
4.交集的概念及符号
5.理解“且”的含义
6.借助“数轴”解决问题
7 补集的概念及数学符号含义
8 补集与交集、并集之间的综合运算
9 利用数轴,求已知集合的补集