

加入时间:2022-05-25

加入时间:2022-06-21

加入时间:2022-05-25

加入时间:2022-05-25

加入时间:2022-05-25

加入时间:2022-05-25

加入时间:2022-05-25
加入时间:2022-05-25

加入时间:2022-05-25

加入时间:2022-05-25

加入时间:2022-05-25

加入时间:2022-05-25

加入时间:2022-05-25

加入时间:2022-05-25
加入时间:2022-05-25

加入时间:2022-05-25
加入时间:2022-05-25

加入时间:2022-05-25
教 案(首页)
编号:YJSD/JWC-17-08
|
课题序号 |
2 |
授课班级 |
联五24工程技术 |
|
授课课时 |
2 |
授课形式 |
新授课 |
|
授课章节 名称 |
§1.2集合之间的关系 |
||
|
使用教具 |
多媒体 |
||
|
教学目的 |
(1)理解集合之间包含及相等的含义,能识别和描述给定集合的子集; (2)结合实例,体会全集与子集的含义. |
||
|
教学重点 |
理解集合之间相等、子集与真子集的含义,会判别集合与集合之间的关系,并能用相应的记号表示; |
||
|
教学难点 |
区分子集与真子集两种关系以及集合与集合和元素与集合之间的关系 |
||
|
更新、补 充、删减 内容 |
无 |
||
|
课外作业 |
课后习题P14 |
||
|
教学后记 |
学生能够掌握集合之间的包含关系及集合相等的含义。能识别给定集合的子集与真子集。 |
||
|
授课主要内容或板书设计 |
|||
|
§1.2集合之间的关系 一、子集 二、真子集 三、集合相等
例题 例题 例题
|
|||
§1.2 集合之间的关系
[学习任务]
1、知识与能力目标:
(1)掌握集合之间的包含关系及集合相等的含义;
(2)能识别给定集合的子集与真子集。
2、过程与方法目标:培养学生应用集合思想解决实际问题的能力
3、情感态度价值观目标:
根据现实情境的探究,激发学生学习数学的兴趣和积极性,陶冶学生的情操,培养实事求是的科学
态度和勇于创新的精神。
[重点和难点] 包含与真包含的区别
[教学模式与方法] 情境问题导向式教学模式
[学习活动] 师生互动
[主要知识点]
一、集合的包含关系
1、子集
(1)定义:一般地,对于两个集合A与B,如果集合A的____________都是集合B的元素,那么集合A叫做集合B的子集,记作_____________________。
(2)性质:A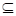 A
即_____________________________
A
即_____________________________
 A 即_____________________________
A 即_____________________________
2、真子集
(1)定义:一般地,对于两个集合A与B,如果集合A是集合B的_________,并且集合B中至少有一个元素____________集合A,那么集合A叫做集合B的真子集,记作_____________________。
(2)性质: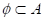 (A为非空集合) 即_____________________________
(A为非空集合) 即_____________________________
注:有限集合元素个数为n,则子集个数为_____________,真子集个数为_____________
3. 集合的相等关系:一般地,如果两个集合的元素________________,那么我们就说这两个集合相等。集合A与集合B相等,记作____________。
1.2.1 子集
引入
元素与集合之间存在着属于或者不属于的关系,集合与集合之间具有怎样的关系呢?
一、问题探究
观察下面各组集合,集合 中的任意一个元素是否都在集合
中的任意一个元素是否都在集合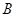 中?
中?
(1) ={0,1},
={0,1},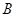 ={
={ ,0,1,2};
,0,1,2};
(2) =N,
=N,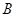 =Z;
=Z;
(3) ={x|x是江苏人},
={x|x是江苏人},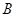 ={x|x是中国人}.
={x|x是中国人}.
可以发现,以上集合 中的任意一个元素都在集合
中的任意一个元素都在集合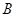 中.
中.
二、抽象概括
1.子集的定义
一般地,对于两个集合 与
与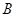 ,如果集合
,如果集合 的任意一个元素都是集合
的任意一个元素都是集合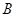 的元素,那么称集合
的元素,那么称集合 是集合
是集合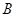 的子集,记作
的子集,记作
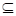
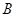 或
或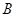
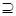
 ,读作“
,读作“ 包含于
包含于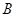 ”或“
”或“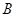 包含
包含 ”.
”.
根据子集的定义,可以得出
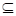
 ,
,
即任何一个集合是它自身的子集.
当集合 中有元素不属于集合
中有元素不属于集合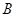 时,则称集合
时,则称集合 不包含于集合
不包含于集合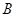 ,或称集合
,或称集合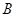 不包含集合A,记作
不包含集合A,记作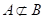 (或
(或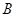
 A).
A).
对于空集,规定
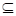
 ,
,
即空集是任何集合的子集.
集合的图形语言:
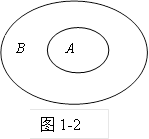 集合常用封闭曲线的内部表示,这种表示集合的图形称为维恩图.集合A
集合常用封闭曲线的内部表示,这种表示集合的图形称为维恩图.集合A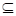 B用维恩图表示如图1-2所示.
B用维恩图表示如图1-2所示.
三、例题讲析
例1 用适当的符号(∈,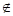 ,
,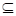 ,
,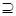 )填空:
)填空:
(1) Z;(2)a
{a,b,c};(3)Q R;
Z;(2)a
{a,b,c};(3)Q R;
(4) {a,b} {a,b,c};(5){0}  ;
;
(6) {x|-1<x<4} {x|0<x<2}.
例2 已知集合 ={a,b,c}.
={a,b,c}.
(1)写出集合 的含一个元素的子集;
的含一个元素的子集;
(2)写出集合 的含两个元素的子集;
的含两个元素的子集;
(3)写出集合 的所有子集.
的所有子集.
四、合作交流
集合 ={1,2,3,4}的子集有哪些?
={1,2,3,4}的子集有哪些?
练习
1.用适当的符号(∈,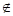 ,
,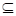 ,
,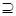 )填空:
)填空:
(1)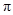 Q;(2)3 {1,2,3};(3)Z
R;
Q;(2)3 {1,2,3};(3)Z
R;
(4) {1,2,3} {1,2};(5) {1,2};
{1,2};
(6) {x|-3<x<5} {x|1<x<4}.
2. 已知集合 ={1,2,3}.
={1,2,3}.
(1)写出集合 的含一个元素的子集;
的含一个元素的子集;
(2)写出集合 的含两个元素的子集;
的含两个元素的子集;
(3)写出集合 的所有子集.
的所有子集.
1.2.2 真子集、相等
一、问题探究
考察下列三组集合,集合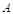 是否是集合
是否是集合 的子集?集合
的子集?集合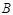 的元素是否都属于集合
的元素是否都属于集合 ?
?
(1) 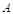 ={a,b},
={a,b}, ={a,b,c,d};
={a,b,c,d};
(2) 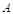 ={1},
={1},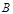 ={x|(x+2)(x-1)=0};
={x|(x+2)(x-1)=0};
(3) 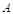 ={x|x是正方形},
={x|x是正方形},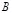 ={x|x是长方形}.
={x|x是长方形}.
可以看出,上述三组集合 、
、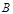 都满足:
都满足:
(1)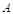
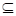
 ;(2)集合
;(2)集合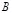 中至少有一个元素不属于集合
中至少有一个元素不属于集合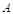 .
.
二、抽象概括
1.真子集的概念
一般地,对于两个集合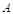 与
与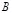 ,如果集合
,如果集合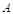 是集合B的子集,并且集合
是集合B的子集,并且集合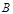 中至少有一个元素不属于集合
中至少有一个元素不属于集合 ,那么称集合
,那么称集合 为集合
为集合 的真子集,记作
的真子集,记作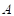

 或
或
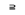 A,读作“
A,读作“ 真包含于
真包含于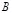 ”或“
”或“ 真包含
真包含 ”.
”.
例如,{a,b,c} {a,b,c,d}, {x|x>4} {x|x>5},
N
{a,b,c,d}, {x|x>4} {x|x>5},
N Z
Z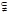 Q
Q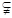 R.
R.
显然,空集是任何非空集合的真子集.
2.集合相等
一般地,如果两个集合的元素完全相同,那么就说这两个集合相等.集合 与集合
与集合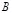 相等,记作
相等,记作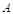 =
=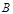 。
。
如{1,2}={2,1}.
符号语言:
如果集合 与集合
与集合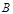 具有相互包含关系,即
具有相互包含关系,即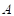
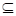
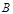 ,且
,且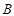
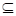
 ,那么这两个集合相等.
,那么这两个集合相等.
三、例题讲析
例3 用适当的符号(∈,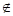 ,
,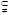 ,
,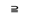 ,=)填空:
,=)填空:
(1)2
N;(2)0
 ;
;
(3){a,b,c} {a,b,c,d,e};
(4){x∈R|x2+x+3=0}  ;
;
(5){x|x是2的倍数} {x|x是4的倍数};
(6){x|x>3} { x|2x-6>0}.
注意:当两个集合既满足包含关系,同时又满足真包含关系,我们考虑真包含关系。
例4 指出下列各组中两个集合的关系.
(1) A={三角形},B={直角三角形};
(2) C={x|x=2k-1,k∈Z},D={x|x=2k+1,k∈Z };
(3)E={x|x是正偶数},F={x|x是偶数}.
例5:已知集合A={a,b,c},写出现满足下列要求的集合A的子集:(1)只有1个元素; (2)有2个元素;(3)与集合A相等; (4)是集合A的真子集。
分析:通过对该题的解答,引导学生学会将问题分类,掌握化归的思想,为求一个集合的子集打基础。
四、合作交流
集合 ={a,b,c}的所有子集中,哪些是它的真子集?
={a,b,c}的所有子集中,哪些是它的真子集?
五、思维拓展
现有面值为1元、2元、5元和10元的人民币各一张.如果取其中的一张或几张,共可以组成多少种不同的币值?
六、课堂小结
1 子集的概念
2 包含符号与属于符号的适用条件