4.2弧度制

学习目标：

1、理解1弧度的角、弧度制的定义

2、掌握角度与弧度的换算[来源:Z§xx§k.Com]

3、熟记特殊角的弧度数

4、掌握弧长公式和扇形面积公式及其运用

教学过程：

一、温故旧知

1、以度、分、秒为单位的角的度量制叫作         。

2、把圆周等分成       份，其中每一份所对应的圆心角为       。

3、任意角：                                                    。

4、角的终边的旋转方向：逆时针方向旋转形成的角是         ；顺时针方向旋转形成的角是         ；零角=       。

5、角度制是       进制，1°=        ；1′=        。

二、探究新知

1、我们能否寻找一种更为便利的度量角的大小的量呢？ 

在同心圆中，同一圆心角所对的弧与它所在圆的半径的比值是一个_________,

这表明弧长与半径的比值与半径无关，而只与_________有关。

2、弧度制的定义：

长度等于半径长的圆弧所对的圆心角，称为____________，记作      ，读作1弧度。这种以弧度为单位来度量角的制度叫做弧度制。

（1）在半径为r的圆中，弧长为的圆弧所对的圆心角为α，则有公式____________；

特别地，在单位圆中，圆心角的弧度数等于弧长，即           。

（2）当考虑角的终边的旋转方向时，正角的弧度数是一个        ，负角的弧度数是一个       ，零角的弧度数是         。

注意：在用弧度制表示角的时候，弧度二字或rad可以略去不写。

3、探究：角度制与弧度制的关系

现在对于同一个角，我们既可以用角度制来表示角，也可以用弧度制来表示。那么两者之间能够相互转化吗？360°是多少弧度？180°呢？90°呢？1°呢？

4、弧度制与角度制的换算

三、例题讲解

例1  把下列各角化为角度与弧度

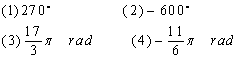
四、新知巩固

练习1  把下列各角化为角度与弧度

练习2  填写下表:

五、新知再探

弧度制下的弧长公式：

          面积公式：

六、快乐体验

练习3  （1）已知扇形的圆心角为60°，半径为3，求圆心角所对弧长及扇形面积。

（2）已知扇形的弧长为10，半径为5，求圆心角及扇形面积。

七、总结回顾

1、弧度制的概念

2、角度制与弧度制的换算

3、弧长公式、扇形面积公式

八、布置作业

1、复习今天新学习的内容

2、记忆特殊角的弧度数

3、课本P137A组习题2、3、4