

加入时间:2022-05-25

加入时间:2022-05-25
加入时间:2022-05-25

加入时间:2022-05-25
加入时间:2022-05-25

加入时间:2022-05-25
加入时间:2022-05-25
加入时间:2023-04-12
加入时间:2022-05-25

加入时间:2022-05-25
加入时间:2022-05-25
加入时间:2022-05-25
加入时间:2022-05-25
加入时间:2022-05-25
减速器运行状态辨识就是根据减速器运行信息识别其状态,对其各部件,因此在信号分析的基础上还需合理的状态辨识方法,完成状态辨识判断主减速器的各部件是否存在故障。
Fisher判别法(Fisher Discriminant Analysis,FDA)的主要思想是将多维数据投影到某个方向上,使总体与总体之间尽可能的分开,再选择合适的判别规则,将新的样品进行分类判别,因为该方法使用了公共协方差矩阵的联合估计量,故含有总体协方差矩阵相等的假定[57]。即是从 个不同状态中抽取
个不同状态中抽取 个特征参数
个特征参数 的样本观测数据,借助方差分析的思想构造一个线性判别函数:
的样本观测数据,借助方差分析的思想构造一个线性判别函数:
|
|
(2-34) |
式中,判别系数 的确定是根据总体的组与组间之间的区分最大,而使每组间的内部间差别最小。
的确定是根据总体的组与组间之间的区分最大,而使每组间的内部间差别最小。
分别针对两种异常状态和多种异常状态的情形说明FDA方法的计算方法。
(1)针对两个总体的情形
假设两种不同状态m和um各具有 个特征参数
个特征参数 的样本观测数据,基于方差分析方法建立线性判别函数:
的样本观测数据,基于方差分析方法建立线性判别函数:
|
|
(2-35) |
根据上述Fisher判别法的系数确定标准,Fisher线性变换的目标函数即为:
|
|
(2-36) |
求解 使得
使得 取得极大值。
取得极大值。
其中 为组间平方和组成的矩阵,
为组间平方和组成的矩阵,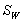 为组内平方和组成的矩阵,分别定义为:
为组内平方和组成的矩阵,分别定义为:
|
|
(2-37) |
|
|
(2-38) |
其中,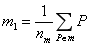 ,
, 。
。
设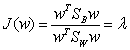 ,则
,则
|
|
(2-39) |
问题转化为一般的求特征值问题,即 为矩阵
为矩阵 特征值,
特征值,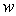 为对应的特征向量。对应上式求得的每一个特征值,都有相应的方差百分比(% of variance),说明此特征向量对应的函数
为对应的特征向量。对应上式求得的每一个特征值,都有相应的方差百分比(% of variance),说明此特征向量对应的函数 所解释的百分比,即
所解释的百分比,即
|
|
(2-40) |
(2)针对多个总体的情形:
减速器的状态辨识中,假定有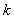 种不同的状态类型
种不同的状态类型
 ,
, ,,…,
,,…, ,其均值和协方差矩阵分别为
,其均值和协方差矩阵分别为 和
和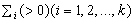 。联立线性判别函数
。联立线性判别函数 ,在
,在 的条件下,有
的条件下,有
|
|
(2-41) |
|
|
(2-42) |
令
|
|
(2-43) |
|
|
(2-44) |
其中,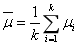 ;
; 。这里
。这里 为一元方差分析中的组间差,
为一元方差分析中的组间差, 则为组内差,应用方差分析的思想,选择
则为组内差,应用方差分析的思想,选择 使得目标函数
使得目标函数
|
|
(2-45) |
达到极大,求得 。
。
基于Fisher判别函数的分类法则:
如果得到的线性判别函数 ,那么对于未知的设备状态Y,定义如下判别规则:
,那么对于未知的设备状态Y,定义如下判别规则:
|
|
(2-46) |
则判别Y来自状态 。
。
当Fisher判别法用于两类区分时,线性变换后得到投影直线,参见图2.7;如果Fisher线性判别扩展应用到多种类别的判别,那么将产生 条投影直线;
条投影直线; 代表类别的个数。
代表类别的个数。

图2.7 两类区分时的Fisher判别法方法示例
Fig.2.7 Example of Fisher’s linear discriminant for two samples
自Zadeh以来,关于可能性理论的研究甚多。可能性的直观方法是由Zadeh提出来的,将可能性理论作为模糊理论的一个扩展而引入的。可能性的直观方法源于模糊约束的概念。以 为论域,
为论域,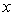 为在
为在 上取值的一个变量,
上取值的一个变量, 为
为 上的一个模糊集。则命题“
上的一个模糊集。则命题“ 为
为 ”可以用隶属度函数
”可以用隶属度函数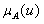 解释为
解释为 时的可能性程度。
时的可能性程度。
模糊理论用于分类即是将模糊性透过可能性测度得到,由隶属函数值的大小确定分类。假设经过Fisher线性变换后同一类别的 值概率分布服从正态分布,即
值概率分布服从正态分布,即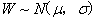 ,其中:
,其中: 为期望,
为期望, 表示标准方差,那么可能性分布函数就可以通过其概率密度函数得出:
表示标准方差,那么可能性分布函数就可以通过其概率密度函数得出:
|
|
(2-47) |
 和
和 的计算如下:
的计算如下:
|
|
(2-48) |
|
|
(2-49) |
图2.8表示概率密度函数(Probability density function)和与之相应的可能性分布函数(Possibility distribution function)的例子。可能性大并不意味着概率大,概率小也不意味着可能性小;但是,当事件不可能发生时,它必不发生,即可能性为0;这就是可能性与概率的不同。值得注意的是,概率仍紧守可加性,即所有概率值的和是1,但可能性无此限制。

图2.8 概率密度函数与可能性分布函数的关系
Fig.2.8 Relationship between the possibility function and the probability function
基于可能性理论的状态辨识,就是将未知状态y对照要判定的某一状态(如判定是否正常),求得状态y“没有状态变化”的可能性。各种领域已经提出很多种模糊推理的方法,状态识别中,需要按照辨识对象的各种条件、依据经验或多次试验决定最合适的模糊推理方法。日本三重大学的陈山鹏教授提出的针对状态识别的模糊推理方法,多次证明了其准确性[58]。
 |
Fig.2.9 State judgement based on possibility theory
如图2.9所示,状态k时得到的无量纲特征参数 的均值和方差分别为
的均值和方差分别为 和
和 ,状态k的可能性分布函数记为
,状态k的可能性分布函数记为 ,相对于状态k的“状态有变化”和“状态有大变化”的可能性分布函数分别为
,相对于状态k的“状态有变化”和“状态有大变化”的可能性分布函数分别为 、
、 和
和 、
、 ;A和B则需要依据设备的类型和重要度通过经验和多次试验来确定。由此决定了识别状态的可能性分布函数。依据状态y(未知状态)的可能性分布函数
;A和B则需要依据设备的类型和重要度通过经验和多次试验来确定。由此决定了识别状态的可能性分布函数。依据状态y(未知状态)的可能性分布函数 和
和 、
、 、
、 对照,可以求得状态变化的可能性。
对照,可以求得状态变化的可能性。
若诊断时状态y的可能性分布函数 与图2.9的可能性分布函数的对照结果为:
与图2.9的可能性分布函数的对照结果为: ,
, ,
, ,则判定结果为与状态k相对比,“状态没有变化”。
,则判定结果为与状态k相对比,“状态没有变化”。