

加入时间:2022-05-25

加入时间:2022-05-25
加入时间:2022-05-25

加入时间:2022-05-25
加入时间:2022-05-25

加入时间:2022-05-25
加入时间:2022-05-25
加入时间:2023-04-12
加入时间:2022-05-25

加入时间:2022-05-25
加入时间:2022-05-25
加入时间:2022-05-25
加入时间:2022-05-25
加入时间:2022-05-25
考虑到齿轮啮合时传递误差、齿轮啮合冲击、齿轮制造精度以及轮系啮合时的受迫振动等因素对轮齿的动、静力接触特性、系统的动态特性、系统传动的精度都有很大的影响,全面地分析减速器轮系各结构参数对啮合受迫振动的影响很有必要。
(1)齿轮副啮合误差分析
齿轮副的力学模型分析如下。建立示图2.1的啮合齿轮副![]() 。设Ⅰ轴匀速旋转,转速为
。设Ⅰ轴匀速旋转,转速为![]() ,则Ⅱ轴的转速
,则Ⅱ轴的转速![]() 。由于齿轮
。由于齿轮![]() 、
、![]() 存在着一定的误差,则
存在着一定的误差,则![]() 齿轮相对于理论转速
齿轮相对于理论转速![]() 有一微量角偏差
有一微量角偏差![]() ,且
,且![]() 为时间
为时间![]() 的周期函数,可表示为
的周期函数,可表示为![]() ,通过单面啮合检查仪检测,
,通过单面啮合检查仪检测,![]() 的变化趋势如图2.2所示。
的变化趋势如图2.2所示。

图2.1 啮合齿轮副
Fig.2.1 Meshing gear pair

图2.2 啮合误差
Fig.2.2 Meshing error
![]() 可分解为两类周期函数
可分解为两类周期函数![]() 和
和![]() ,即
,即
|
|
(2-5) |
![]() 为“大周期”误差,对应其旋转频率
为“大周期”误差,对应其旋转频率![]() 较小,由此引起的附加动载荷也很小,它主要影响的是动态传动链的精度,暂不考虑。
较小,由此引起的附加动载荷也很小,它主要影响的是动态传动链的精度,暂不考虑。![]() 为“小周期”误差,,其交变频率为啮合频率:
为“小周期”误差,,其交变频率为啮合频率:
|
|
(2-6) |
显然![]() 引起的附加动载荷会比较大,这类误差在齿轮系的运行中的作用也比较大。
引起的附加动载荷会比较大,这类误差在齿轮系的运行中的作用也比较大。
将![]() 展开成傅里叶级数:
展开成傅里叶级数:
|
|
(2-7) |
|
或
|
(2-8) |
只考虑基频,令![]() ,则
,则
|
|
(2-9) |
![]() 的变化取决于齿轮副的啮合精度。
的变化取决于齿轮副的啮合精度。
由于轮系是具有质量和刚度的扭振系统,在![]() 的作用下轮系将产生受迫振动。
的作用下轮系将产生受迫振动。
(2)齿轮轴的扭振分析
图2.3为电动汽车减速器用到的齿轮轴Ⅱ,由多台阶构成,轴上装有齿轮等圆盘形零件,可视作集中转动惯量![]() ,轴的极惯性矩为:
,轴的极惯性矩为:
|
|
(2-10) |

图2.3 齿轮轴Ⅱ
Fig.2.3 Gear shaft Ⅱ
设在轴的从动轮![]() 处输入扰动
处输入扰动![]() ,则轴处于扭振状态,各段轴的扭振可用微分方程表示:
,则轴处于扭振状态,各段轴的扭振可用微分方程表示:
|
|
(2-11) |
|
|
(2-12) |
![]() 为轴的切变模量(N/m2);
为轴的切变模量(N/m2);![]() 为轴的材料密度(kg/m3);
为轴的材料密度(kg/m3);![]() 为扭振的传播速度(m/s)。
为扭振的传播速度(m/s)。
用![]() 和
和![]() 分别表示
分别表示![]() 由正向和负向无限接近
由正向和负向无限接近![]() 。由轴的连续条件
。由轴的连续条件
|
|
(2-13) |
在区间![]() 内式(2-13)通解为:
内式(2-13)通解为:
|
|
(2-14) |
因![]() ,故上式可写为:
,故上式可写为:
|
|
(2-15) |
通过简单的坐标变换,上式可以推广到各个轴段,如区间![]()
|
|
(2-16) |
轴的扭振计算归结为无量纲参数![]() 的计算,将
的计算,将![]() 为定义为振形参数。
为定义为振形参数。
通过相邻两轴段的关系计算![]() 。取
。取![]() 为分离体,计算过程可参加下图2.3(b)所示,其两端分别作用有
为分离体,计算过程可参加下图2.3(b)所示,其两端分别作用有![]() 和
和![]() ,则
,则
|
|
(2-17) |
|
|
(2-18) |
|
|
(2-19) |
根据扭转变形胡克定律,并将上式简化得到
|
|
(2-20) |
由上式可知,计算各段的![]() 值,须由轴的两端开始。如图2.3(c)轴,为了便于计算,将
值,须由轴的两端开始。如图2.3(c)轴,为了便于计算,将![]() 的左端取做
的左端取做![]() 的正向,
的正向,![]() 的右端取为
的右端取为![]() 的正向,则可依次求得
的正向,则可依次求得![]() 和
和![]() 。
。
若在![]() 处输入扰动
处输入扰动![]() 时,必然同时存在着扰动力矩
时,必然同时存在着扰动力矩![]() ,若求得
,若求得![]() 、
、![]() ,即可推导
,即可推导![]() 与
与![]() 之关系。取
之关系。取![]() 为分离体,如图2.3(c),由牛顿第二定律可求得扰动力矩:
为分离体,如图2.3(c),由牛顿第二定律可求得扰动力矩:
|
|
(2-21) |
|
|
(2-22) |
定义![]() 为动态惯量,与
为动态惯量,与![]() 有相同的量纲,其值决定于轴的质量、刚度和扰动频率。
有相同的量纲,其值决定于轴的质量、刚度和扰动频率。
(3)轮系的固有频率
电动汽车的二级传动主减速器的传动系统由两根齿轮轴构成,见图2.4。Ⅰ轴的动力由电动机通过柔性传动装置传递,Ⅱ轴为减速器中间轴,分析轮系的固有振动频率。
由传动链的终端开始,由式(2-21),以频率![]() 将Ⅱ轴转化为Z2处的动态惯量为
将Ⅱ轴转化为Z2处的动态惯量为![]() ,则Z1作用于Z2的扰动力矩为
,则Z1作用于Z2的扰动力矩为
|
|
(2-23) |

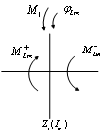
|
图2.4 齿轮传动简图 Fig.2.4 The diagram of gear transmission |
图2.5 分离体Z1的受力图 Fig.2.5 The free-body diagram of detached body Z1 |
设Z1扭振的振幅为![]() ,则
,则
|
|
(2-24) |
|
|
(2-25) |
取Z1为分离体如图2.5所示,基于牛顿第二定律
|
|
(2-26) |
|
|
即 |
|
(2-27) |
|
令 |
|
(2-28) |
|
则 |
|
(2-29) |
由此,通过公式即可将整个轮系向其中任一断面转化而得总动态量![]() ,
,![]() 包含了整个轮系的质量与刚度,对于一个结构尺寸已确定的轮系,
包含了整个轮系的质量与刚度,对于一个结构尺寸已确定的轮系,![]() 是频率
是频率![]() 的函数,由
的函数,由![]() ,可得到轮系的固有频率。
,可得到轮系的固有频率。
通过对减速器振动特性分析,对于减速器的设计在理论上得出以下结论:
(1)应尽可能提高齿轮的齿形加工精度,能够提高减速器的传动平稳性。
(2)随着齿轮圆周线速度的增大,附加动载荷和角速度的波动显著增加;当啮合频率接近轮系的固有频率时,将引发齿轮的啮合共振,应予以避免;
(3)通过改变齿轮轴的质量、刚度等参数,使齿轮轴的固有振荡频率远离主减速器工作频率范围,避免齿轮轴扭振的发生。
(4)在不过分提高齿轮的制造精度、增加生产成本的前提下,适当改变轮系的结构参数,达到较好的质量、刚度的匹配,改善传动的平稳性,提高汽车的传动效率;这样既不增加生产成本,又能提高系统的传动质量。