课题：三次函数的切线问题

高二数学备课组  韦君

一、教学分析和学情分析

从初中接触函数开始，初中阶段学生学习并掌握了一次函数，二次函数，反比例函数的图像以及相关性质，进入高中后，高一阶段逐步学习了指对函数，幂函数，三角函数等其他的基本初等函数。而三次函数作为幂函数中最基本的函数，学生在高一阶段只是了解它的大概图形以及最基本的一些特征（比如对称性，奇偶性），在导数这个“工具”下，我们可以进一步研究三次函数的其他性质（比如单调性的导数法证明，切线问题，切割线性质，三次方程的韦达定理等）。

本节课由周测中出现的三次函数的切线方程出发，进一步研究过某个点三次函数的切线条数问题，通过学生的任务型合作探究过程从特殊到一般解决问题，并结合作图以及GGB软件演示感受猜想的结论，最终再从代数角度加以论证。

二、教学目标

1.学生通过任务型小组合作探究，会求出具体过某些点的三次函数的切线方程或判断条数，这个过程中养了数学运算和数据分析能力；

2.学生通过对自己探究结果的作图和GGB软件的展示进行直观想象，大胆地猜测和感受；

3.学生通过尝试代数论证自己猜想的结论来提升自我的逻辑推理能力.

三、教学重点和难点

重点：求解或判断三次函数过某点切线的条数；

难点：从代数角度论证

四、教学过程

【周测回顾：T17】已知曲线，                 【学生活动】

求：（1）曲线在点处的切线方程；                  投影学生的优秀作答，

（2）曲线过点的切线方程.                        并由学生总结两小题的

                                                          区别以及解题步骤.

【小结】1.画出学生解答答案（利用希沃自带作图软件）； 2.感受两条切线的不同.

【任务型合作探究】已知曲线                 【学生活动】

1.任意选取一个定点；（每组至少取两个）                  1.小组合作取点研究任务；

2.求出过这个定点曲线的切线方程或判断出切线条数；     2.每组派代表利用平板同步希沃

3.观察其他组的选择情况；                                 当堂展示研究结果；

4.一共发现几种不同的情况？并尝试用作图展示；           3.展示不同结果；

【拓展探究】已知函数                       【学生活动】

（2）设，如果过点可作曲线的三条     学生合作论证并展示讲解

切线，证明：

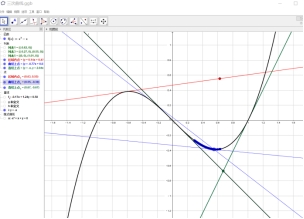
【GGB展示】利用GGB软件动画展示不同位置切线条数，让学生感受规律.

五、板书设计：

三次函数的切线问题

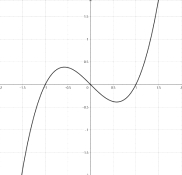
【任务型合作探究】已知曲线                       

1.任意选取一个定点；（每组至少取两个）                        

2.求出过这个定点曲线的切线方程或判断出切线条数；            

3.观察其他组的选择情况；                                         

4.一共发现几种不同的情况？并尝试用作图展示；                  

5.拓展探究引出切线规律

六、教后感