2.2基本不等式

《基本不等式》在人教A版高中数学第一册第二章第2节，本节课的内容是基本不等式的形式以及推导和证明过程。本章一直在研究不等式的相关问题，对于本节课的知识点有了很好的铺垫作用。同时本节课的内容也是之后基本不等式应用的必要基础。

课程目标

1.掌握基本不等式的形式以及推导过程，会用基本不等式解决简单问题。

2.经历基本不等式的推导与证明过程，提升逻辑推理能力。

3.在猜想论证的过程中，体会数学的严谨性。

数学学科素养

1.数学抽象：基本不等式的形式以及推导过程；

2.逻辑推理：基本不等式的证明；

3.数学运算：利用基本不等式求最值；

4.数据分析：利用基本不等式解决实际问题；

5.数学建模：利用函数的思想和基本不等式解决实际问题，提升学生的逻辑推理能力。

重点：基本不等式的形成以及推导过程和利用基本不等式求最值；

难点：基本不等式的推导以及证明过程．

教学方法：以学生为主体，采用诱思探究式教学，精讲多练。

教学工具：多媒体。

一、 情景导入：

在前面一节，已经学了重要不等式，那么将重要不等式中各个式子开方变形，会得到什么呢？

要求：让学生自由发言，教师不做判断。而是引导学生进一步观察.研探.

二、预习课本，引入新课

阅读课本44-45页，思考并完成以下问题

1. 重要不等式的内容是？

2.基本不等式的内容及注意事项？

3.常见的不等式推论？

要求：学生独立完成，以小组为单位，组内可商量，最终选出代表回答问题。

三、新知探究

1.重要不等式

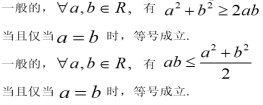
2.基本不等式

(1)基本不等式成立的条件:_____________.

(2)等号成立的条件:当且仅当______时取等号. 

注意：一正二定三等.

3.几个重要的不等式

(1)a²+b²≥______(a,b∈R).

(2)       ≥____(a,b同号).

(3)   (a,b∈R).

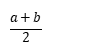
(4)               (a,b∈R).

4. 设a>0,b>0，则a,b的算术平均数为___________,几何平均

 数为______，基本不等式可叙述为：_____________________.

四、典例分析、举一反三

题型一    利用基本不等式求最值

例1 求下列各题的最值.

（1）已知x>0,y>0,xy=10,求          的最小值；

（2）x>0,求          的最小值；

（3）x<3，求             的最大值；

【答案】见解析

【解析】（1）  由x>0,y>0,xy=10.

当且仅当2y=5x,即x=2,y=5时等号立.

(2)∵x>0, 等号成立的条件是         即x=2,

∴f(x)的最小值12.

(3)∵x<3,∴x-3<0,∴3-x>0,

 

 

当且仅当           即x=1时，等号成立.故f(x)的最大值为-1. 

解题技巧：（利用基本不等式求最值）

(1)通过变形或“1”的代换，将其变为两式和为定值或积为定值；

(2)根据已知范围，确定两式的正负符号；

(3)根据两式的符号求积或和的最值.

总而言之，基本不等式讲究“一正二定三等”.

跟踪训练一

（1）已知x>0,y>0，且         求x+y 的最小值；

（2）已知x<   求函数               的最大值;

（3）若x,y∈(0,+∞)且2x+8y-xy=0,求x+y的最小值.

【答案】见解析

 

 

 

 

 

 

 

 

 

 

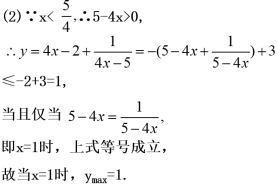
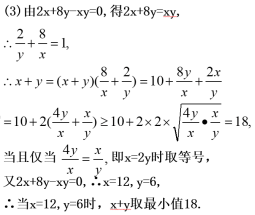
题型二   利用基本不等式解决实际问题

例2　（ １ ） 用篱笆围一个面积为１００的矩形菜园 ,当这个矩形的边长为多少时 ， 所用篱笆最短？ 最短篱笆的长度是多少？

（ ２ ） 用一段长为 ３６ｍ 的篱笆围成一个矩形菜园 ,当这个矩形的边长为多少时 ， 菜园的面积最大？ 最大面积是多少？

【答案】见解析

【解析】设矩形菜园的相邻两条边的长分别为，篱笆的长度为m.

(1)由已知由 ≥，可得所以,

当且仅当=10时，上式等号成立.

(2)由已知得，矩形菜园的面积为

由 =  = 9,可得81，当且仅当=9时，上式等号成立.

解题技巧：(利用基本不等式解决实际问题)

设出未知数x,y,根据已知条件，列出关系式，然后利用函数的思想或基本不等式解决相应的问题。（注意运用基本不等式讲究“一正二定三等”）

 

跟踪训练二

1. 如图所示，将一矩形花坛扩建成一个更大的矩形花坛，要求点在上，点在上，且对角线过点，已知米，米.

（1）要使矩形的面积大于50平方米，则的长应在什么范围？

（2）当的长为多少米时，矩形花坛的面积最小？并求出最小值.

【答案】见解析

【解析】（1）设的长为米，则米

        

由矩形的面积大于得：

又，得：，解得：或

即长的取值范围为：

（2）由（1）知：矩形花坛的面积为：

当且仅当，即时，矩形花坛的面积取得最小值

故的长为米时，矩形的面积最小，最小值为平方米

五、课堂小结

让学生总结本节课所学主要知识及解题技巧

六、板书设计

 

 

 

 

七、作业

课本48页习题2.2

本节课主要采用讲练结合与分组探究的教学方法，坚持“以学生为主体，以教师为主导”的原则，先通过几何证明基本不等式，在充分了解基本不等式的含义后，再进一步运用其求最值。切记：利用基本不等式的条件是一正二定三等。