弧度制

同学们：森林公园内的摩天轮、钱塘江的潮汐现象、一年四季，这些现象有一个共同的特征——周而复始，循环往复。你还能举例符合这个特征的现象吗？一周7天，简谐振动等等。生活中很多这种现象，三角函数模型能更好更科学解释这些现象，继任意角之后，我们来研究新的内容——弧度制，为研究三角函数做好准备。

   现实生活中，度量长度的单位有哪些？米、英寸、尺。定义好了一米以后，就可以用米作为单位来度量长度；

   角度的单位是什么？1度角是怎么规定的呢？（初中是分周角）

（几何画板）：分周角，相邻射线与圆心形成的角1度。若等分圆周呢？也行

         涉及的弧长，半径，圆心角满足的关系为：

       只要将圆周等分成360份，圆变大变小，每段弧所对的角始终是1度吗？

（再总结）将圆周等分成360份，每段弧所对的角是1度，这其实就是一个单位角，用它作为标准就可以度量其他的角。并且，它不会随着圆的大小变化而变化，所以它非常客观、科学。 谁首先创造——古巴比伦人，为什么360？ 中国古代

份。这些都是前人的工作，那我们也可以建立新的度量制度啊。要建立新度量制度，先必须对什么作规定？——单位，单位角

       现在，就请你穿越千年，到古巴比伦人前面，你来分圆周，你会分成几份？

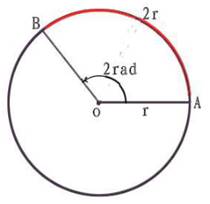
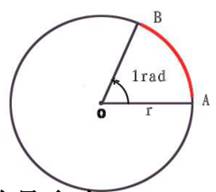
长度为l的弧呢？  ，角从度数变成了一个十进制的数，计算方便。从角度制到弧度制，从六十进制到十进制，道路是漫长且艰辛的，历经千年，由欧拉创立。

 有了两种度量角度的制度，那一个很自然的问题来了？两种度量制如何换算？

例1.把下列弧度化为角度

（1）   （2）3.5

例2.把下列角度化为弧度

（1）  （2）

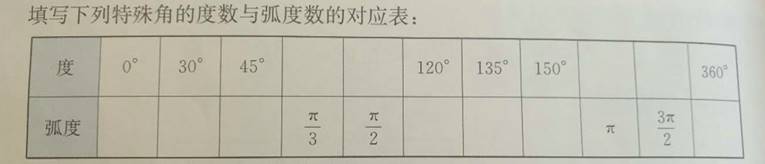
正角的弧度数正，负角，零角；每个角度都有唯一实数与之对应，反过来，每一个实数也有唯一的角度与之对应，说明角的集合和实数集之间建立起了一一对应。角的集合是数集，函数值的集合也是数集，数集到数集，这为什么作了铺垫？

例3.利用弧度制证明下列关于扇形的公式

（1）  （2）   （2）