高二数学——5.3.2　第1课时　函数的极值

学习目标　1.了解函数极值的概念，会从几何方面直观理解函数的极值与导数的关系.2.掌握函数极值的判定及求法.3.掌握函数在某一点取得极值的条件．

一、函数极值的概念

问题1　如图是某处群山的截面图，你能指出山峰、山谷吗？

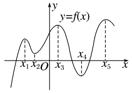
问题2　你能描述一下在各个山峰、山谷附近的特点吗？

知识梳理

极值点与极值的概念

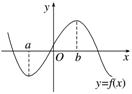
1．极小值点与极小值

函数y＝f(x)在点x＝a的函数值f(a)比它在点x＝a附近其他点的函数值都小，f′(a)＝0；而且在点x＝a的左侧______，右侧________，则把a叫做函数y＝f(x)的____________，f(a)叫做函数y＝f(x)的________．

2．极大值点与极大值

函数y＝f(x)在点x＝b的函数值f(b)比它在点x＝b附近其他点的函数值都大，f′(b)＝0；而且在点x＝b的左侧________，右侧________，则把b叫做函数y＝f(x)的____________，f(b)叫做函数y＝f(x)的__________．

3．极大值点、极小值点统称为________，极大值和极小值统称为________．

例1　函数y＝f(x)的导函数的图象如图所示，给出下列判断：

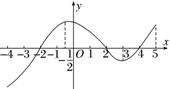
①函数y＝f(x)在区间(3,5)内单调递增；②函数y＝f(x)在区间内单调递减；

③函数y＝f(x)在区间(－2,2)内单调递增；④当x＝－时，函数y＝f(x)有极大值；

⑤当x＝2时，函数y＝f(x)有极大值．

则上述判断中正确的序号是________．

二、求函数的极值

例2　求下列函数的极值：

(1)f(x)＝x³－3x²－9x＋5；

(2)f(x)＝x－alnx(a∈R)．

反思感悟　函数极值和极值点的求解步骤

跟踪训练2　求下列函数的极值：

(1)f(x)＝x³－x；

(2)f(x)＝x²e^－x.

三、由极值求参数的值或范围

例3　(1)若函数f(x)＝x³＋ax²＋bx＋a²在x＝1处取得极值10，则a＝________，b＝________.

(2)已知函数f(x)＝x³－(m＋3)x²＋(m＋6)x(x∈R，m为常数)，在区间(1，＋∞)内有两个极值点，求实数m的取值范围．

跟踪训练3　若函数f(x)＝x³－4x＋4的图象与直线y＝a恰有三个不同的交点，则实数a的取值范围是________．

1.函数f(x)的定义域为R，它的导函数y＝f′(x)的部分图象如图所示，则下面结论错误的是(　　)

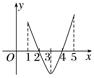
A．在(1,2)上函数f(x)单调递增

B．在(3,4)上函数f(x)单调递减

C．在(1,3)上函数f(x)有极大值

D．x＝3是函数f(x)在区间[1,5]上的极小值点

2．(多选)已知函数f(x)＝2x³＋ax²＋36x－24在x＝2处有极值，则该函数的一个单调递增区间是(　　  )

A．(－∞，2)    B．(3，＋∞)    C．(2，＋∞)       D．(－∞，3)

3．设函数f(x)＝xe^x，则(　　)

A．x＝1为f(x)的极大值点

B．x＝1为f(x)的极小值点

C．x＝－1为f(x)的极大值点

D．x＝－1为f(x)的极小值点

4．已知曲线f(x)＝x³＋ax²＋bx＋1在点(1，f(1))处的切线斜率为3，且x＝是y＝f(x)的极值点，则a＝________，b＝________.