6.3.2 二项式系数的性质   

本节课选自《2019人教A版高中数学选择性必修第三册》，第六章《计数原理》，本节课主本节课主要学习二项式系数的性质

本节是在学习了二项式定理的基础上，探究二项式系数的性质。由于二项式系数组成的数列就是一个离散型函数，引导学生从函数的角度研究二项式系数的性质，便于建立知识前后联系，使学生运用利用几何直观、数形结合、特殊到一般的数学思想进行思考。

研究二项式系数这组特定的性质，对巩固二项式定理，建立知识间的联系，进一步认识组合数、进行组合数的计算和变形都有重要作用，对后续学习微分方程也具有重要地位。

 

课程目标	学科素养
A.能记住二项式系数的性质,并能灵活运用性质解决相关问题. B.会用赋值法求二项展开式系数的和,注意区分项的系数和二项式系数.	1.数学抽象：二项式系数的性质 2.逻辑推理：运用函数的观点讨论二项式系数的单调性 3.数学运算：运用二项式性质解决问题 4.几何直观：运用函数图像讨论二项式系数的性质

重点： 二项式系数的性质（对称性、增减性与最大值和各二项式系数的和）； 

难点：理解增减性与最大值时，根据n的奇偶性确定相应的分界点；

利用赋值法证明二项式系数的性质，数学思想方法的渗透.

一、 温故知新

1．二项式定理

(a＋b)ⁿ＝_________________________ (n∈N^*)．

(1)这个公式所表示的规律叫做二项式定理．

(2)展开式：等号右边的多项式叫做(a＋b)ⁿ的二项展开式，展开式中一共有______项．

(3)二项式系数：各项的系数____ (k∈{0,1,2，…，n})叫做二项式系数．

Cn(0)aⁿ＋Cn(1)a^n－1b＋Cn(2)a^n－2b²＋…＋Cn(k)a^n－kb^k＋…＋Cn(n)bⁿ

n＋1 ；Cn(k)

2．二项展开式的通项公式

(a＋b)ⁿ展开式的第______项叫做二项展开式的通项，记作T_k＋1＝______.

k＋1 ；Cn(k)a^n－kb^k

二、 新知探究

探究1：计算展开式的二项式系数并填入下表

二项式系数:  

通过计算、填表、你发现了什么规律？

n	的展开式的二项式系数
1	1	1
2	1	2	1
3	1	3	3	1
4	1	4	6	4	1
5	1	5	10	10	5	1
6	1	6	15	20	15	6	1

将上表写成如下形式：

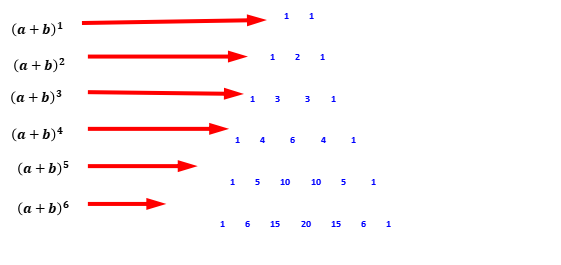思考：通过上表和上图，能发现什么规律？

展开式的二项式系数

  

我们还可以从函数的角度分析它们。可看成是以为自变量的函数，其定义域是

我们还可以画出它的图像。

例如，当时，

函数()的图像是7个离散的点，如图所示。

1.对称性

与首末两端“等距离”的两个二项式系数相等,即

.

2.增减性与最大值

当k<时,随k的增加而增大;由对称性可知,当k>时,随k的增加而减小.当n是偶数时,中间的一项取得最大值;当n是奇数时,中间的两项相等,且同时取得最大值.

探究2.已知 = 

3.各二项式系数的和

+…+=2ⁿ.

令x=1 得=

所以，的展开式的各二项式系数之和为

1. 在(a+b)⁸的展开式中,二项式系数最大的项为　　　　　,在(a+b)⁹的展开式中,二项式系数最大的项为　　　　　　　　. 

解析:因为(a+b)⁸的展开式中有9项,所以中间一项的二项式系数最大,该项为a⁴b⁴=70a⁴b⁴.

因为(a+b)⁹的展开式中有10项,所以中间两项的二项式系数最大,这两项分别为a⁵b⁴=126a⁵b⁴,a⁴b⁵=126a⁴b⁵.

答案:1.70a⁴b⁴　126a⁵b⁴与126a⁴b⁵　

2. A=+…与B=+…的大小关系是(　　)

A.A>B　　　B.A=B　　　C.A<B　　　D.不确定

解析:∵(1+1)ⁿ=+…+=2ⁿ,

(1-1)ⁿ=-…+(-1)ⁿ=0,

∴+…=+…=2^n-1,即A=B.

答案:B

三、典例解析

类型1　求二项式系数或系数最大的项

　在x2(2)⁸的展开式中：

(1) 系数的绝对值最大的项是第几项？

(2) 求二项式系数最大的项；

(3) 求系数最大的项．

【解答】 T_r＋1＝C8(r)·()^8－r·x2(－2)^r＝(－1)^r·C8(r)·2^r· (r＝0,1,2，…，8)．

(1) 设第r＋1项系数的绝对值最大，则·2r－1，(r－1)所以，(1)

解得5≤r≤6.又因为0≤r≤8，r∈N，所以r＝5或r＝6，故系数的绝对值最大的项是第6项和第7项．

(2) 二项式系数最大的项为中间项，即第5项，T₅＝C8(4)·2⁴·＝1 120x^－6.

(3) 由(1)知展开式中第6项和第7项的系数的绝对值最大，而第6项的系数为负，第7项的系数为正，所以系数最大的项为T₇＝C8(6)·2⁶·x^－11＝1 792x^－11.

　若(1＋2x)ⁿ的展开式中第6项与第7项的系数相等，求展开式中二项式系数最大的项和系数最大的项．

【解答】 T₆＝Cn(5)(2x)⁵，T₇＝Cn(6)(2x)⁶，依题意有Cn(5)2⁵＝Cn(6)2⁶，解得n＝8.故(1＋2x)⁸的展开式中，二项式系数最大的项为T₅＝C8(4)·(2x)⁴＝1 120x⁴.设第k＋1项系数最大，则有

·2k＋1(k＋1)⇒5≤k≤6，又k∈{0,1,2，…，8}，故k＝5或k＝6.故系数最大的项为T₆＝1 792x⁵，T₇＝1 792x⁶.

【规律总结】 (1) 注意“系数最大”“二项式系数最大”及“系数绝对值最大”的区别．

(2) 要求展开式的系数的最大值，在系数均为正数的前提下，只需比较相邻两个系数的大小，即设第r＋1项的系数最大，则Tr＋1的系数≥Tr＋2的系数.(Tr＋1的系数≥Tr的系数，)

类型2　整除或余数问题

　(1) 求证：1＋2＋2²＋…＋2^5n－1能被31整除(n∈N^*)；

(2) 求S＝C27(1)＋C27(2)＋…＋C27(27)除以9的余数．

【解答】 (1) 1＋2＋2²＋…＋2^5n－1＝2－1(25n－1)＝2⁵ⁿ－1＝32ⁿ－1＝(31＋1)ⁿ－1＝Cn(0)×31ⁿ＋Cn(1)31^n－1＋…＋Cn(n－1)×31＋Cn(n)－1＝31(Cn(0)×31^n－1＋Cn(1)×31^n－2＋…＋Cn(n－1))，显然上式括号内的数为整数，所以原式能被31整除．

(2) S＝C27(1)＋C27(2)＋…＋C27(27)＝2²⁷－1＝8⁹－1＝(9－1)⁹－1＝C9(0)×9⁹－C9(1)×9⁸＋…＋C9(8)×9－C9(9)－1＝9(C9(0)×9⁸－C9(1)×9⁷＋…＋C9(8))－2＝9(C9(0)×9⁸－C9(1)×9⁷＋…＋C9(8)－1)＋7，显然上式括号内的数是正整数，故S除以9的余数是7.

【规律总结】 在利用二项式定理证明整除问题或求余数问题时，要进行合理的变形，常用的变形方法是拆数，往往是将幂底数写成两数和或差的形式，其中的一个数是除数或其正整数倍．

课本例3.求证:在的展开式中,奇数项的二项式系数的和等于偶数项的二项式系数的和.

证明:在展开式

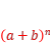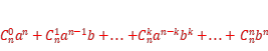=中，

令a=1,b=-1，得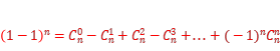

即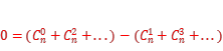

因此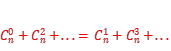

即在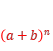的展开式中，奇数项的二项式系数的和等于偶数项的二项式系数的和.

二项展开式中系数和的求法

(1)对形如(ax+b)ⁿ,(ax²+bx+c)^m(a,b,c∈R,m,n∈N^*)的式子求其展开式的各项系数之和,常用赋值法,只需令x=1即可;对(ax+by)ⁿ(a,b∈R,n∈N^*)的式子求其展开式各项系数之和,只需令x=y=1即可.

(2)一般地,若f(x)=a₀+a₁x+a₂x²+…+a_nxⁿ,则f(x)展开式中各项系数之和为f(1),

奇数项系数之和为a₀+a₂+a₄+…=,

偶数项系数之和为a₁+a₃+a₅+…=.

类型3　“赋值法”的应用

跟踪训练1(课本例3补充)已知(1－2x)⁷＝a₀＋a₁x＋a₂x²＋…＋a₇x⁷，求下列各式的值．

(1) a₁＋a₂＋…＋a₇；

(2) a₁＋a₃＋a₅＋a₇；

(3) a₀＋a₂＋a₄＋a₆.

【解答】 令x＝1，

则a₀＋a₁＋a₂＋a₃＋…＋a₇＝－1.①

令x＝－1，则a₀－a₁＋a₂－…－a₇＝3⁷.②

(1) 令x＝0，得a₀＝1，代入①中得a₁＋a₂＋a₃＋…＋a₇＝－2.

(2) 由①－②得2a₁＋2a₃＋2a₅＋2a₇＝－1－3⁷，所以a₁＋a₃＋a₅＋a₇＝2(－1－37)＝－1 094.

(3) 由①＋②得2a₀＋2a₂＋2a₄＋2a₆＝－1＋3⁷，所以a₀＋a₂＋a₄＋a₆＝2(－1＋37)＝1 093.

　本例条件下，求|a₀|＋|a₁|＋|a₂|＋…＋|a₇|.

【解答】 方法一：因为(1－2x)⁷的展开式中，a₀，a₂，a₄，a₆大于零，而a₁，a₃，a₅，a₇小于零，所以|a₀|＋|a₁|＋|a₂|＋…＋|a₇|＝(a₀＋a₂＋a₄＋a₆)－(a₁＋a₃＋a₅＋a₇)＝1 093－(－1 094)＝2 187.

方法二：|a₀|＋|a₁|＋|a₂|＋…＋|a₇|是(1＋2x)⁷展开式中各项的系数和，令x＝1，所以|a₀|＋|a₁|＋…＋|a₇|＝3⁷＝2 187.

【规律总结】 “赋值法”是解决二项式系数问题的常用的方法，根据题目要求，灵活赋给字母所取的不同值．一般地，要使展开式中项的关系变为系数的关系，令x＝0可得常数项，令x＝1可得所有项系数之和，令x＝－1可得奇次项系数之和与偶次项系数之和的差，而当二项展开式中含负数时，令x＝－1则可得各项系数绝对值之和．

课堂评价及时反馈

1. 二项式(1＋x)⁵的展开式中，各项二项式系数的和是(　D　)

A. 2 B. 8

C. 16 D. 32

【解析】 二项式(1＋x)⁵的展开式的各项二项式系数的和是2⁵＝32.

2. 已知x(3)ⁿ的展开式中，各项系数的和与其各项二项式系数的和之比为64，则n等于(　C　)

A. 4 B. 5

C. 6 D. 7

【解析】 令x＝1，得各项系数的和为4ⁿ，二项式系数的和为2ⁿ，故有2n(4n)＝64，所以n＝6.

3. 在二项式x(1)ⁿ的展开式中恰好第3项的二项式系数最大，则展开式中的常数项是__6__.

【解析】 由展开式中恰好第3项的二项式系数最大，可知n＝4，则展开式的通项为T_r＋1＝C4(r)x^4－rx(1)^r＝C4(r)(－1)^rx^4－2r，令4－2r＝0，解得r＝2，所以常数项是T₃＝C4(2)(－1)²＝6.

4. 已知(1＋x)ⁿ的展开式中，第3项与第11项的二项式系数相等，则二项式系数和是(　A　)

A. 2¹²  B. 2¹¹ 

C. 2¹⁰  D. 2⁹

【解析】 因为Cn(2)＝Cn(10)，所以n＝12，所以二项式系数和是2¹².

5. (多选)设二项式x(1)ⁿ的展开式中第5项是含x的一次项，那么这个展开式中系数最大的项是(　CD　)

A. 第8项 B. 第9项

C. 第10项 D. 第11项

【解析】 因为展开式的第5项为T₅＝，所以令3(n－4)－4＝1，解得n＝19，所以展开式中系数最大的项是第10项和第11项．

 

四、小结

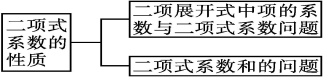
五、课时练

 

本节课需要学生探究的内容比较多，由于学生的数学基础比较薄弱，所以在教学过程中教师不仅要耐心的指导，还要努力创设一个轻松和谐的课堂氛围，让每个学生都能大胆的说出自己的想法，保证每个学生都能学有所得。为了让每个学生在课上都能有话说，还需要学生做到课前预习，并且教师要给学生提出明确的预习目标。