6.2  组合数

一．知识梳理

组合数与组合数公式

1.组合数的定义:从n个不同元素中取出m(m≤n)个元素的所有不同组合的个数,

叫做从n个不同元素中取出m个元素的组合数,

用符号 表示.

例如，从3个不同元素中取出2个元素的组合数，表示为，

从4个不同元素中取出3个元素的组合数，表示为.

思路：从4个不同元素中取出3个元素的组合数，设这4个元素为a,b,c,d，那么从中取出3个元素的排列数 =24，以“元素相同”为标准将这24个排列分组如图，一共有4组，因此组合数 =4.

问题3：前面已经提到，组合和排列有关系，我们能否利用这种关系，由排列数来求组合数呢？

 

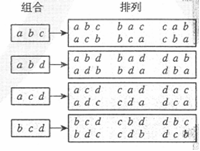
也可以这样理解，求“从4个元素中取出3个元素的排列数”

第1步，从4个元素中取出3个元素作为一组，共有种不同的取法；
第2步，将取出的3个元素做全排列，共有种不同的取法.
于是，根据分布乘法计数原理有
=

即

==4.

同样的从个不同对象中取出个做排列，可以分成两个步骤完成，第一步从个不同对象中取出 个，有种选法；

第二步将选出的个对象做全排列，有种排法.

由分步乘法计数原理有 ，所以

 

上述公式称为组合数公式.

2.组合数公式:,这里n,m∈N^*,并且m≤n.

另外,我们规定=1.

二、典例解析

课本例6.计算：

（1）；（3）

解:根据组合数公式，可得

（1）   120;

（2）  

(3)

(4)

    观察例6的（1）与（2），（3）与（4）的结果，你有什么发现？（1）与（2）分别用了不同形式的组合数公式，你对公式的选择有什么想法？

1.公式(m,n∈N^*,且m≤n),一般用于求值计算.

2.公式(m,n∈N^*,且m≤n),一般用于化简证明.在具体选择公式时,要根据题目特点正确选择.

3.根据题目特点合理选用组合数的两个性质,能起到简化运算的作用,需熟练掌握.

类型1　组合数的公式

　(课本例6补充)(1) 计算：C100(98)＋C200(199).

(2) 计算：C3(3)＋C4(3)＋C5(3)＋…＋C20(3).

(3) 解方程：①Cx²＋3x＋2₁₆＝C16(5x＋5)；

②3Cx－3(x－7)＝5Ax－4(2).

【解答】 (1) C100(98)＋C200(199)＝C100(2)＋C200(1)＝2(100×99)＋200＝4 950＋200＝5 150.

(2) C3(3)＋C4(3)＋C5(3)＋…＋C20(3)＝C4(4)＋C4(3)＋C5(3)＋…＋C20(3)＝C5(4)＋C5(3)＋…＋C20(3)＝…＝C21(4)＝5 985.

(3) ①因为Cx²＋3x＋2₁₆＝C16(5x＋5)，

所以x²＋3x＋2＝5x＋5或x²＋3x＋2＋5x＋5＝16，即x²－2x－3＝0或x²＋8x－9＝0，

所以x＝－1或x＝3或x＝－9或x＝1.

经检验：x＝3或x＝－9不合题意舍去．

故原方程的解是x₁＝－1，x₂＝1.

②由排列数和组合数公式，原方程可化为

3·(x－7)！·4！((x－3)！)＝5·(x－6)！((x－4)！)，

则4！(3(x－3))＝x－6(5)，即(x－3)(x－6)＝40，

所以x²－9x－22＝0，解得x＝11或x＝－2(舍去)．所以方程的根为x＝11.

【规律总结】 在利用组合数公式进行计算、化简时，要灵活运用组合数的性质，一般地，计算Cn(m)时，若m比较大，可利用性质1，不计算Cn(m)而改为计算Cn(n－m)，在计算组合数之和时，常利用性质2.

　已知n－3(3)＝5(19)，求n的值．

【解答】 原方程可变形为n－3(3)＋1＝5(19)，

所以Cn－1(5)＝5(14)·Cn－3(3)，

即5！((n－1)(n－2)(n－3)(n－4)(n－5))＝5(14)·3！((n－3)(n－4)(n－5))，化简并整理得n²－3n－54＝0，解得n＝9或n＝－6(不合题意，舍去)，所以n＝9.

课本例7. 在100件产品中，有98件合格品，2件次品.从这100件产品中任意抽出3件.

（1）有多少种不同的抽法？

（2）抽出的3件中恰好有1件是次品的抽法有多少种？

（3）抽出的3件中至少有1件是次品的抽法有多少种？  

分析:（1）所求的不同抽法的种数，就是从100件产品中取出3件的组合数；

（2）分两步，第一步从2件次品中抽出1件次品，第二步从98件合格品中抽出2件合格品，由乘法原理可得；

（3）可从反面考虑，其反面是抽出的3件全是合格品，求出方法数后，由第（1）题的结论减去这个结果即可得．

解：（1）所求的不同抽法的种数，就是从100件产品中取出3件的组合数，∴共有(种)；

（2）从2件次品中抽出1件次品的抽法有种，

从98件合格品中抽出2件合格品的抽法有种，

因此抽出的3件中恰好有1件次品的抽法有(种).

（3）抽出的3件产品中至少有1件是次品的抽法的种数，

也就是从100件中抽出3件的抽法种数减去3件中都是合格品的抽法的种数，

即(种).

组合问题的基本解法

(1)判断是否为组合问题;

(2)是否分类或分步;

(3)根据组合的相关知识进行求解.

类型2　有限制条件的组合问题

　(课本例7补充)现有男运动员6名，女运动员4名，其中男、女队长各1名．选派5人外出参加比赛，则在下列情形中各有多少种选派方法？

(1) 男运动员3名，女运动员2名；

(2) 队长中至少有1人参加；

(3) 既要有队长，又要有女运动员．

【解答】 (1) 分两步完成：第一步，选3名男运动员，有C6(3)种选法；第二步，选2名女运动员，有C4(2)种选法．由分步乘法计数原理可得，共有C6(3)·C4(2)＝120种选法．

(2) 方法一(直接法)：“只有男队长”的选法种数为C8(4)；“只有女队长”的选法种数为C8(4)；“男、女队长都入选”的选法种数为C8(3)，所以共有2C8(4)＋C8(3)＝196种选法．

方法二(间接法)：从10人中任选5人有C10(5)种选法，其中不选队长的方法有C8(5)种，所以“至少有1名队长”的选法有C10(5)－C8(5)＝196种．

(3) 当有女队长时，其他人任意选，共有C9(4)种选法；当不选女队长时，必选男队长，共有C8(4)种选法，其中不含女运动员的选法有C5(4)种，所以不选女队长时的选法共有(C8(4)－C5(4))种．故既要有队长又要有女运动员的选法共有C9(4)＋C8(4)－C5(4)＝191种．

【规律总结】 组合问题常有以下两类题型：

(1) “含有”或“不含有”某些元素的组合题型：“含”，则先将这些元素取出，再由另外元素补足；“不含”，则先将这些元素剔除，再从剩下的元素中去选取．

(2) “至少”或“至多”含有几个元素的组合题型：解这类题必须十分重视“至少”与“至多”这两个关键词的含义，谨防重复与漏解．用直接法和间接法都可以求解，通常用直接法分类复杂时，考虑逆向思维，用间接法处理．

类型3　组合中的分组、分配问题

　已知有6本不同的书，求按下列条件各有多少种不同的方法．

(1) 分给甲、乙、丙三人，每人两本；

(2) 分为三份，每份两本．

【解答】 (1) 根据分步乘法计数原理可得C6(2)C4(2)C2(2)＝90种．

(2) 分给甲、乙、丙三人，每人两本有C6(2)C4(2)C2(2)种方法，这个过程可以分两步完成：第一步分为三份，每份两本，设有x种方法；第二步再将这三份分给甲、乙、丙三名同学有A3(3)种方法．由分步乘法计数原理可得C6(2)C4(2)C2(2)＝xA3(3)，所以x＝3(3)＝15.因此分为三份，每份两本一共有15种不同分配方法．

【规律总结】 (1) 解决这类问题的关键是分清分组问题还是分配问题．

(2) 分组问题属于“组合”问题，常见的分组问题有三种：①完全均匀分组，每组的元素个数均相等．②部分均匀分组，应注意不要重复，有n组均匀，最后必须除以n！.③完全非均匀分组，这种分组不考虑重复现象．

(3) 分配问题属于“排列”问题，分配问题可以按要求逐个分配，也可以分组后再分配．

　6本不同的书分为3组，求在下列条件下各有多少种不同的分配方法．

(1) 一组1本，一组2本，一组3本(不平均分组)；

(2) 一组4本，另外两组各1本(局部平均分组)．

【解答】 (1) 一组1本，一组2本，一组3本的分组种数为C6(3)C3(2)C1(1)＝20×3＝60.

(2) 一组4本，另外两组各1本的分组种数为2(2)＝2(15×2)＝15.

课堂评价及时反馈

1. 下列计算结果是21的是(　D　)

A. A4(2)＋C6(2)  B. C7(3)

C. A7(2)  D. C7(2)

【解析】 A4(2)＋C6(2)＝2！(4！)＋2！4！(6！)＝12＋15＝27，C7(3)＝3！4！(7！)＝35，A7(2)＝5！(7！)＝42，C7(2)＝2！5！(7！)＝21.

2. 从10名学生中挑选出3名学生参加数学竞赛，不同的选法有(　C　)

A. A10(3)种 B. 3!

C. C10(3)种 D. 以上均不对

【解析】 从10名学生中挑选出3名学生参加数学竞赛，没有顺序，是组合问题．

3. (2022·新高考Ⅰ卷)从2至8的7个整数中随机取2个不同的数，则这2个数互质的概率为(　D　)

A. 6(1)  B. 3(1) 

C. 2(1)  D. 3(2)

【解析】 从2至8的7个整数中随机取2个不同的数，共有C7(2)＝21种不同的取法，若两数不互质，不同的取法有：(2,4)，(2,6)，(2,8)，(3,6)，(4,6)，(4,8)，(6,8)，共7种，故所求概率P＝21(21－7)＝3(2).

4. (多选)在100件产品中，有98件合格品，2件不合格品，从这100件产品中任意抽出3件，则抽出的3件产品中(　CD　)

A. 至多有1件不合格品的抽法种数为C2(1)C98(2)

B. 都是合格品的抽法种数为C100(3)

C. 至少有1件不合格品的抽法种数为C2(1)C98(2)＋C2(2)C98(1)

D. 至少有1件不合格品的抽法种数为C100(3)－C98(3)

【解析】 对于A，分两种情况：①抽出的3件产品都是合格品，抽法种数为C98(3)；②抽出的3件产品中有1件不合格品，抽法种数为C2(1)C98(2)，所以所求抽法种数为C98(3)＋C2(1)C98(2)，故A错误，B错误．对于C，分两种情况：①抽出的3件产品中有1件不合格品，抽法种数为C2(1)C98(2)；②抽出的3件产品中有2件不合格品，抽法种数为C2(2)C98(1)，所以所求抽法种数为C2(1)C98(2)＋C2(2)C98(1)，故C正确．对于D，用“排除法”，知抽法种数为C100(3)－C98(3)，故D正确．

5. 一个口袋内装有大小相同的7个白球和1个黑球．

(1) 从口袋内取出3个球，有多少种取法？

(2) 从口袋内取出3个球，使其中含有1个黑球，有多少种取法？

(3) 从口袋内取出3个球，使其中不含黑球，有多少种取法？

【解答】 (1) 从口袋内的8个球中取出3个球，取法种数是C8(3)＝3×2×1(8×7×6)＝56.

(2) 从口袋内取出3个球有1个是黑球，于是还要从7个白球中再取出2个，取法种数是C7(2)＝2×1(7×6)＝21.

(3) 由于所取出的3个球中不含黑球，也就是要从7个白球中取出3个球，取法种数是C7(3)＝3×2×1(7×6×5)＝35.

 

四、小结

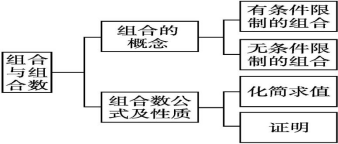
五、课时练

在本节课的教学中，学生可能遇到的问题（或困难、障碍）是学生对组合概念的理解，并能区分出组合与排列。要解决这一问题，就要要通过典型的、学生比较熟悉的实例，经过概括得出组合的定义，然后借助计数原理好排列数，推导出组合数公式，其中关键是在具体情境中运用组合解决计数问题。