6.2.1  排列

本节课选自《2019人教A版高中数学选择性必修第三册》，第六章《计数原理》，本节课主本节课主要学习排列与排列数。

排列与组合是在学习了两个计数原理之后，由于排列、组合及二项式定理的研究都是以两个计数原理为基础，同时排列和组合又能进一步简化和优化计数问题。教学的重点是排列的理解，利用计数原理推导排列数公式，难点是运用排列解决实际问题。

课程目标	学科素养
A. 理解并掌握排列、排列数的概念,能用列举法、树状图法列出简单的排列. B.掌握排列数公式及其变式,并能运用排列数公式熟练地进行相关计算. C.掌握有限制条件的排列应用题的一些常用方法,并能运用排列的相关知识解一些简单的排列应用题.	1.数学抽象：排列的概念 2.逻辑推理：排列数的性质 3.数学运算：运用排列数解决计数问题 4.数学建模：将计数问题转化为排列问题

 

重点：理解排列的定义及排列数的计算

难点：运用排列解决计算问题

一、 温故知新

两个原理的联系与区别

1.联系:分类加法计数原理和分步乘法计数原理都是解决计数问题最基本、最重要的方法.

2.区别

	分类加法计数原理	分步乘法计数原理
区别一	完成一件事共有n类办法,关键词是“分类”	完成一件事共有n个步骤,关键词是“分步”
区别二	每类办法中的每种方法都能独立地完成这件事,它是独立的、一次的且每种方法得到的都是最后结果,只需一种方法就可完成这件事	除最后一步外,其他每步得到的只是中间结果,任何一步都不能独立完成这件事,缺少任何一步也不能完成这件事,只有各个步骤都完成了,才能完成这件事
区别三	各类办法之间是互斥的、并列的、独立的	各步之间是关联的、独立的,“关联”确保不遗漏,“独立”确保不重复

 

问题1.  从甲、乙、丙三名同学中选出2人参加一项活动，其中1名同学参加上午的活动，另1名同学参加下午的活动.

分析：要完成的一件事是“选出2名同学参加活动，1名参加上午的活动，另1名参加下午的活动”，可以分两个步骤：

第1步，确定上午的同学，从3人中任选1人，有3种选法；

第2步，确定下午的同学，只能从剩下的2人中去选，有2种选法.

根据分步乘法计数原理，不同的选法种数为3×2=6.

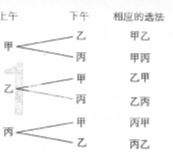
问题如果把上面问题中被取出的对象叫做元素，则问题可叙述为：从3个不同的元素中任意取出2个，并按一定的顺序排成一列，共有多少种不同的排列方法？

问题2. 从1,2,3,4这4个数字中选出3个能构成多少个无重复数字的三位数？

分析：从4个数中每次取出三个按“百位、十位、个位” 的顺序排成一列，就得到一个三位数.因此有多少种不同的排列方法就有多少个不同的三位数，可以分三个步骤解决：

第1步，确定百位上的数字，从1、2、3、4这4个数中任取一个，有4种方法；第2步，确定十位上的数字，只能从余下的3个数字中取，有3种方法；第3步，确定个位上的数字，只能从余下的2个数字中取，有2种方法；根据分步乘法计数原理，从1、2、3、4这4个不同的数字中，每次取出3个数字，按百位、十位、个位的顺序排成一列，不同的排列方法为4×3×2=24

因而共可得到24个不同的三位数，如图所示

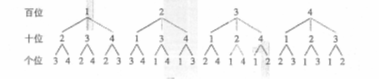
   同样，问题2可以归结为：

      从4个不同的元素中任意取出3个，并按一定的顺序排成一列，共有多少种不同的排列方法？所有不同的排列是

不同的排列方法为4×3×2=24

上述问题1,2的共同特点是什么？你能将它们推广到一般情形吗？

一、排列的相关概念

1.排列:一般地,从n个不同元素中取出m(m≤n)个元素,并按照一定的顺序排成一列,叫做从n个不同元素中取出m个元素的一个排列.

2.相同排列:两个排列的元素完全相同,且元素的排列顺序也相同.

名师点析理解排列应注意的问题

(1)排列的定义中包括两个基本内容,一是“取出元素”,二是“按一定顺序排列”.

(2)定义中的“一定顺序”说明了排列的本质:有序.

二、典例解析

类型1　判断是否为排列问题

　(1) 北京、上海、天津三个民航站之间的直达航线的飞机票的价格(假设来回的票价相同)；

(2) 选2个小组分别去植树和种菜；

(3) 选2个小组去种菜；

(4) 选10人组成一个学习小组；

(5) 选3个人分别担任班长、学习委员、生活委员；

(6) 某班40名学生在假期相互通信．

【解答】 (1) 中票价只有三种，虽然机票是不同的，但票价是一样的，不存在顺序问题，所以不是排列问题．

(2) 植树和种菜是不同的，存在顺序问题，属于排列问题．

(3)(4) 不存在顺序问题，不属于排列问题．

(5) 中每个人的职务不同，例如甲当班长或当学习委员是不同的，存在顺序问题，属于排列问题．

(6) A给B写信与B给A写信是不同的，所以存在顺序问题，属于排列问题．

所以在上述各题中(2)(5)(6)属于排列问题．

【规律总结】 判断一个具体问题是否为排列问题，就看取出元素后排列是有序的还是无序的，而检验它是否有序的依据就是变换元素的“位置”(这里的“位置”应视具体问题的性质和条件来决定)，看其结果是否有变化，有变化就是排列问题，无变化就不是排列问题．

课本例1. 某省中学足球队赛预选赛每组有6支队，每支队都要与同组的其他各队在主、客场分别比赛1场，那么每组共进行多少场比赛？

分析：每组任意2支队之间进行的1场比赛，可以看作是从该组6支队中选取2支，按“主队、客队”的顺序排成的一个排列.

解：可以先从这6支队中选1支为主队，然后从剩下的5支队中选1支为客队.按分步乘法计数原理，每组进行的比赛场数为

6×5=30.

类型2　“树形图”(列表法)枚举排列问题

　(课本例1补充)(1) 北京、广州、南京、天津4个城市相互通航，则有多少种机票？

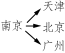
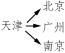
【解答】 列出每一个起点和终点情况，如图(1)所示．

   

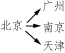
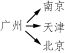
　　　　　　　　　　　　(例2(1))

故符合题意的机票种类有：北京广州，北京南京，北京天津，广州南京，广州天津，广州北京，南京天津，南京北京，南京广州，天津北京，天津广州，天津南京，共12种．

(2) 从语文、数学、英语、物理4本书中任意取出3本分给甲、乙、丙三人，每人一本，试将所有不同的分法列举出来．

【解答】 从语文、数学、英语、物理4本书中任意取出3本，分给甲、乙、丙三人，每人一本，相当于从4个不同的元素中任意取出3个元素，按“甲、乙、丙”的顺序进行排列，每一个排列就对应着一种分法，所以共有4×3×2＝24种不同的分法．不妨给“语文、数学、英语、物理”编号，依次为1,2,3,4，画出树形图如图(2)所示．

　　　

(例2(2))

由树形图可知，按甲、乙、丙顺序分的分法为：

语数英　语数物　语英数　语英物　语物数　语物英　数语英　数语物　数英语　数英物　数物语　数物英　英语数　英语物　英数语　英数物　英物语　英物数　物语数　物语英　物数语　物数英　物英语　物英数．

【规律总结】 在画树形图时，先以安排哪个元素在首位为分类标准进行分类，在每类中，再按余下元素在前面元素不变的情况下，定第二位并按序分类，依次一直进行到完成一个排列，最后应把所有排列列举出来．

课本例2. （1）一张餐桌上有5盘不同的菜，甲、乙、丙3名同学每人从中各取1盘菜，共有多少种不同的取法？

（2）学校食堂的一个窗口共卖5种菜，甲、乙、丙3名同学每人从中选一种，共有多少种不同的选法？

分析：3名同学每人从5盘不同的菜中取1盘菜，可看作是从这5盘菜中任取3盘，放在3个位置（给3名同学）的一个排列；而3名同学每人从食堂窗口的5种菜中选1种，每人都有5种选法，不能看成一个排列.

解： （1）可以先从这5盘菜中取1盘给同学甲，然后从剩下的4盘菜中取1盘给同学乙，最后从剩下的3盘菜中取1盘给同学丙.按分步乘法计数原理，不同的取法种数为

5×4×3=60.

（2）可以先让同学甲从5种菜中选1种，有5种选法；再让同学乙从5种菜中选1种，也有5种选法；

最后让同学丙从5种菜中选1种，同样有5种选法.

按分步乘法计数原理，不同的取法种数为

5×5×5=125.

类型3　无限制条件的排列问题

　(课本例2补充)(1) 沪宁高铁线上有六个大站：上海、苏州、无锡、常州、镇江、南京，铁路部门应为沪宁线上的六个大站(这六个大站之间)准备不同的火车票的种数为(　B　)

A. 15　　 B. 30　　

C. 12　　 D. 36

【解析】 对于两个大站A和B，从A到B的火车票与从B到A的火车票不同，因为每张车票对应一个起点站和一个终点站，因此，每张火车票对应从6个不同元素(大站)中取出2个不同元素(起点站和终点站)的一种排列，故不同的火车票有6×5＝30(种)．

(2) 6名同学报名参加两个课外活动小组，每名同学限报其中一个小组，则不同的报名方法有__64__种．(用具体数字作答)

【解析】 由题意，6名同学报名参加两个课外活动小组，每名同学限报其中的一个小组，则每名同学都有两种报名方法，则这6名同学共有2⁶＝64种不同的报名方法．

【规律总结】 排列的概念很清楚，要从“n个不同的元素中取出m个元素”. 即在排列问题中元素不能重复选取，而在用分步乘法计数原理解决的问题中，元素可以重复选取．

课堂评价及时反馈

1. 下列问题中是排列问题的是(　A　)

A. 由1,2,3三个数字组成无重复数字的三位数

B. 从40人中选5人组成篮球队

C. 从100人中选2人抽样调查

D. 从1,2,3,4,5中选2个数组成集合

2. (多选)下列问题是排列问题的是(　AD　)

A. 求从甲、乙、丙三名同学中选出两名分别参加数学、物理兴趣小组的方法种数

B. 求从甲、乙、丙三名同学中选出两名参加一项活动的方法种数

C. 求从a，b，c，d中选出3个字母的方法种数

D. 求从1,2,3,4,5中取出2个数字组成两位数的个数

【解析】 对于A，从甲、乙、丙三名同学中选出两名分别参加数学、物理兴趣小组，与顺序有关，是排列问题；对于B，从甲、乙、丙三名同学中选出两名参加一项活动，只要求选出即可，不是排列问题；对于C，从a，b，c，d中选出3个字母，只要求选出即可，不是排列问题；对于D，从1,2,3,4,5中取出2个数字组成两位数，需要先选出再排序，是排列问题．

3. 从1,2,3,4这四个数字中任取两个不同的数字，则可组成的不同两位数有(　B　)

　　　　　　　　　　　　　　　

 

A. 9个 B. 12个

C. 15个 D. 18个

【解析】 画出树形图如图，由此可知共有12个．

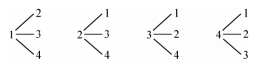
 (第3题)

4. 从a，b，c，d，e五个元素中每次取出三个元素，可组成以b为首的不同排列的个数为(　C　)

A. 6 B. 10

C. 12 D. 16

【解析】 画出树形图如图，可知共12个，它们分别是bac，bad，bae，bca，bcd，bce，bda，bdc，bde，bea，bec，bed.

 

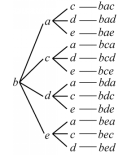
(第4题)

5. 在1,2,3,4的排列a₁a₂a₃a₄中，满足a₁>a₂，a₃>a₂，a₃>a₄的排列的个数是__5__.

【解析】 首先注意a₁位置的数比a₂位置的数大，可以借助树形图进行筛选．满足a₁>a₂的树形图如图(1)：

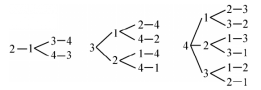
 (第5题(1))

其次满足a₃>a₂的树形图如图(2)：

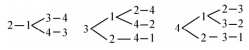
 (第5题(2))

最后满足a₃>a₄的排列有2143,3142,3241,4132,4231，共5个．