6.1分类加法计数原理与分步乘法计数原理(2)

本节课选自《2019人教A版高中数学选择性必修第三册》，第六章《计数原理》，本节课主要学习分类加法计数原理与分步乘法计数原理。

两个计数原理，其核心是准确理解两个原理，弄清它们的区别。理解它关键就是要根据实例概括两个计数原理。学生对计数问题已经有一些经验和技巧，本节课的内容分类计数原理和分步计数原理就是在此基础上的发展。由于排列、组合及二项式定理的研究都是以两个计数原理为基础,所以在本学科计数问题中有重要的地位，是本学科的核心内容。教学的重点是两个原理的理解与应用，解决重点的关键是从单一到综合，恰当安排实例。

课程目标	学科素养
A. 进一步理解和掌握分类加法计数原理和分步乘法计数原理； B．能应用两个计数原理解决实际问题.	1.数学抽象：两个计数原理 2.逻辑推理：运用分类思想解决复杂问题 3.数学运算：运用计数原理解决计数问题 4.数学建模：将计数问题转化为分类和分步计数问题

 

重点： 分类加法计数原理、分步乘法计数原理及其简单应用

难点： 准确应用两个计数原理解决问题

一、 温故知新

两个原理的联系与区别

1.联系:分类加法计数原理和分步乘法计数原理都是解决计数问题最基本、最重要的方法.

2.区别

	分类加法计数原理	分步乘法计数原理
区别一	完成一件事共有n类办法,关键词是“分类”	完成一件事共有n个步骤,关键词是“分步”
区别二	每类办法中的每种方法都能独立地完成这件事,它是独立的、一次的且每种方法得到的都是最后结果,只需一种方法就可完成这件事	除最后一步外,其他每步得到的只是中间结果,任何一步都不能独立完成这件事,缺少任何一步也不能完成这件事,只有各个步骤都完成了,才能完成这件事
区别三	各类办法之间是互斥的、并列的、独立的	各步之间是关联的、独立的,“关联”确保不遗漏,“独立”确保不重复

 

二、典例解析

类型1　两个计数原理在组数中的应用

课本例5．给程序模块命名，需要用个字符，其中首字符要求用字母或，后两个要求用数字.问最多可以给多少个程序命名？

分析：要完成一件事是“给一个程序模块命名” ，可以分三个步骤完成：第1步，首选字符，第2步，选中间字符；第3步，选最后一个字符，还有首字符又可以分为两类。

解：由分类加法计数原理，首字符不同选法的种数为，后两个字符从中选，因为数字可以重复，

所以不同选法的种数都为9.

由分步乘法计数原理，不同名称的个数是，

即最多可以给1053个程序命名.

跟踪训练1(课本例5补充)用0,1，…，9这十个数字，可以组成多少个：

(1) 三位整数？

(2) 无重复数字的三位整数？

【解答】 由于0不可在最高位，因此应对它进行单独考虑．

(1) 百位数字有9种选择，十位数字和个位数字都各有10种选择．由分步乘法计数原理知，满足题意的三位数共有9×10×10＝900个．

(2) 由于数字不可重复，可知百位数字有9种选择，十位数字也有9种选择，但个位数字仅有8种选择．由分步乘法计数原理知，满足题意的三位数共有9×9×8＝648个．

【规律总结】 排数问题实际就是分步问题，需要用分步乘法计数原理解决．此题中，由于数字“0”的出现，又进行了分类讨论，即在解决相关的排数问题时，要注意两个计数原理的综合应用．

类型2　两个计数原理在涂色中的应用

　现有4种不同颜色，要对如图所示的四个部分A，B，C，D进行着色，要求有公共边界的两部分不能用同一种颜色，则不同的着色方法共有(　D　)

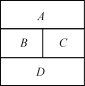
(例2)

A. 24种 B. 30种

C. 36种 D. 48种

【解析】 因为A，B，C之间不能同色，A与D可以同色，因此要分类讨论A，D同色与不同色这两种情况， 故不同的着色方法种数为4×3×2＋4×3×2×1＝48.

【规律总结】 解决涂色问题的一般思路：

(1) 按涂色的顺序分步进行，用分步乘法计数原理计数．

(2) 按颜色恰当选取情况分类，用分类加法计数原理计数．

(3) 注意相邻区域同色与不同色的情况．

类型3　放球(填数字、排序)问题

将编号1,2,3,4的小球放入编号为1,2,3的盒子中，要求不允许有空盒子，且球与盒子的号不能相同，则放球方法有(　B　)

A. 16种 B. 12种

C. 9种 D. 6种

课本例4. 要从甲、乙、丙3幅不同的画中选出2幅，分别挂在左、右两边墙上的指定位置，

问共有多少种不同的挂法？

分析：要完成的一件事是“从3幅画中选出2幅，并分别挂在左、右两边墙上”，可以分步完成.

解：从3幅画中选出2幅分别挂在左、右两边墙上，

可以分两个步骤完成:

第1步，从3幅画中选1幅挂在左边墙上，有3种选法，

第2步，从剩下的2幅画中选1幅挂在右边墙上，有2种选法，

根据分步乘法计数原理，不同挂法的种数是

N=3×2=6.

(课本例4补充)某校高一年级有四个班，四位老师各教一个班的数学，在该年级某次数学考试中，要求每位数学老师均不在本班监考，则不同的安排方法种数为(　B　)

A. 8 B. 9

C. 12 D. 24

【解析】 (1) 由题意可知，这四个小球有两个小球放在一个盒子中，当1与2号球放在同一盒子中时，有2种不同的放法；当1与3号球放在同一盒子中时，有2种不同的放法；当1与4号球放在同一盒子中时，有2种不同的放法；当2与3号球放在同一盒子中时，有2种不同的放法；当2与4号球放在同一盒子中时，有2种不同的放法；当3与4号球放在同一盒子中时，有2种不同的放法．因此，不同的放球方法有12种．

(2) 设四个班分别是A，B，C，D，对应的数学老师分别是a，b，c，d.让a老师先选，可从B，C，D班中选一个，有3种选法，不妨假设a老师选的是B，则b老师从剩下的三个班级中任选一个，有3种选法，剩下的两位老师都只有1种选法. 由分步乘法计数原理知，共有3×3×1×1＝9种不同的安排方法．

【规律总结】 解答此类问题，首先必须弄清是“分类”还是“分步”，其次要搞清“分类”或“分步”的具体标准是什么，选择合理的标准处理事件，关键是看能否独立完成这件事，避免计数的重复或遗漏．

例6. 电子元件很容易实现电路的通与断、电位的高与低等两种状态，而这也是最容易控制的两种状态.因此计算机内部就采用了每一位只有0或1两种数字的记数法，即二进制.为了使计算机能够识别字符，需要对字符进行编码，每个字符可以用一个或多个字节来表示，其中字节是计算机中数据存储的最小计量单位，每个字节由8个二进制位构成.问：

（1）一个字节(8位)最多可以表示多少个不同的字符？

（2）计算机汉字国标码(GB码)包含了6763个汉字，一个汉字为一个字符，要对这些汉字进行编码，每个汉字至少要用多少个字节表示？

分析： （1）要完成的一件事是“确定1个字节各二进制位上的数字” .由于每个字节有8个二进制位，每一位上的值都是0，1两种选择，而且不同的顺序代表不同的字符，因此可以用分步乘法计数原理来求解；（2）只要计算出多少个字节所能表示的不同字符不少于6763个即可.

解：（1）一个字节共有8位，每位上有2种选择，根据分步乘法计数原理，一个字节最多可以表示

2×2×2×2×2×2×2×2==256个不同的字符；

（2）由（1）知，用一个字节能表示256个字符，

∵256<6763，一个字节不够；根据分步乘法计数原理，

2个字节可以表示256×256=65536个不同的字符，

∵65536>6763，所以每个汉字至少要用2个字节表示.

1.使用两个原理的原则

使用两个原理解题时,一定要从“分类”“分步”的角度入手.“分类”是对于较复杂应用问题的元素分成互相排斥的几类,逐类解决,用分类加法计数原理;“分步”就是把问题分化为几个互相关联的步骤,然后逐步解决,这时可用分步乘法计数原理.

2.应用两个计数原理计数的四个步骤

(1)明确完成的这件事是什么.

(2)思考如何完成这件事.

(3)判断它属于分类还是分步,是先分类后分步,还是先分步后分类.

(4)选择计数原理进行计算.

解决抽取(分配)问题的方法

(1)当涉及对象的数目不大时,一般选用列举法、树状图法、框图法或图表法.

(2)当涉及对象的数目很大时,一般有两种方法:①直接使用分类加法计数原理或分步乘法计数原理.一般地,若抽取是有顺序的,则按分步进行;若是按对象特征抽取的,则按分类进行.②间接法.去掉限制条件,计算所有的抽取方法数,然后减去所有不符合条件的抽取方法数即可.

 

课堂评价及时反馈

1. 由数字1,2,3组成的无重复数字的整数中，偶数的个数为(　D　)

A. 15 B. 12

C. 10 D. 5

【解析】 分三类，第一类组成一位整数，偶数为2，共1个；第二类组成两位整数，其中偶数为12和32，共2个；第三类组成三位整数，其中偶数为132和312，共2个．由分类加法计数原理知共有5个偶数．

2. 有3名防控新冠肺炎疫情的志愿者，每人从2个不同的社区中选择1个进行服务，则不同的选择方法共有(　C　)

A. 12种 B. 9种

C. 8种 D. 6种

【解析】 每名防控新冠肺炎疫情的志愿者都有2种不同的选择方法，根据分步计数原理可知，不同的选择方法共有2³＝8种．

3.  某年级要从3名男生，2名女生中选派3人参加某次社区服务，如果要求至少有1名女生，那么不同的选派方案有(　D　)

A. 6种 B. 7种

C. 8种 D. 9种

【解析】 可按女生人数分类：若选派1名女生，有2×3＝6种方案；若选派2名女生，有3种方案．由分类加法计数原理知，共有9种不同的选派方案．

4. (多选)有4名同学报名参加三个不同的社团，则下列说法正确的是(　AC　)

A. 每名同学限报其中一个社团，则不同的报名方法共有3⁴种

B. 每名同学限报其中一个社团，则不同的报名方法共有4³种

C. 每个社团限报1名同学，则不同的报名方法共有24种

D. 每个社团限报1名同学，则不同的报名方法共有3³种

【解析】 对于A，B，每1名同学都有3种报法，则由分步计数原理知共有3⁴种报名方法，故A正确，B错误．对于C，D，第一个社团有4种选择方法，第二个社团有3种选择方法，第三个社团有2种选择方法，根据分步计数原理知共有4×3×2＝24种方法，故C正确，D错误．

5.  用0,1,2,3,4,5可以组成无重复数字的比2 000大的四位奇数有 120 个．

【解析】 按末位是1,3,5分三类，第一类：末位是1，共有4×4×3＝48个；第二类：末位是3，共有3×4×3＝36个；第三类：末位是5，共有3×4×3＝36个．由分类加法计数原理知，共有48＋36＋36＝120个．

 

四、小结

五、课时练

在本节课的教学中，学生可能遇到的问题（或困难、障碍）是综合应用两个计数原理，产生这一问题的原因是不能根据问题的特征选择对应的原理。要解决这一问题，就要要通过典型的、学生比较熟悉的实例，经过概括得出两个计数原理，然后从单一到综合的方式，安排例题，其中关键是从单一到综合，引导学生体会两个计数原理的基本思想。