一题一课，以题研课

江苏省宜兴市张渚高级中学  陈云明

摘要：高三数学复习中，习题课是其中最重要的一种表现形式，而“一题一课”教学，可以整合教师的有效备课、学生的主体参与，更有效地发挥习题课效益，减轻课业负担，提升复习质量，引领并指导复习备考．

关键词：一题一课；一题多解；一题多变；变式；复习

课堂是教学的主阵地，数学课堂应该有一定的广度、深度，特别是高三复习课，更要精心选好试题，针对知识点，完善知识结构，激活学生思维，探究能力深度．其中，“一题一课”教学是高三数学复习课中一种非常重要的表现形成，对“题”进行深度挖掘，以“原题”为本，根据学生的认知规律和知识结构，合理设置，巧妙引导，从多层面进行“一题多解”尝试，从多角度进行“一题多变”创新，由浅入深，浅显易懂，做一题，得一法，会一类，通一片，触类旁通．

1．一题多解

一题多解是在教师精心挑选下，利用同一道题目引导学生用不同的思维方法来破解，利用发散、联想、类比等思维方法对题目进行多角度、多方位的分析与思考，利用不同的知识、不同的方法、不同的工具等来分析与处理问题．一题多解能有效促进数学知识之间的联系，提升数学思维能力，提高思维的创新力与创新应用能力等．

例1．（2020年高考数学江苏卷第11题）设{a_n}是公差为d的等差数列，{b_n}是公比为q的等比数列．已知数列{a_n+b_n}的前n项和S_n=n²－n+2ⁿ－1（n∈N*），则d+q的值是________．

分析：此题以两个特殊类型的等差数列与等比数列加以融合与交汇，结合两数列对应项的和式{a_n+b_n}的前n项和的表达式来确定对应数列的公差d与公比q的和式的值问题．

思维视角一：代数运算

方法1：（代数运算法）

解析：当n=1时，S₁=a₁+b₁=1－1+2－1=1；

当n≥2时，a_n+b_n=S_n－S_n－1=n²－n+2ⁿ－1－[（n－1）²－（n－1）+2^n－1－1]=2^n－1+2n－2，

则有a₂+b₂=2^2－1+2×2－2=4，a₃+b₃=2^3－1+2×3－2=8，a₄+b₄=2^4－1+2×4－2=14，

而a₂+b₂=a₁+d+b₁q=4，a₃+b₃=a₁+2d+b₁q²=8，a₄+b₄=a₁+3d+b₁q³=14，

将a₁+b₁=1与以上三式依次对应相减，

可得d+b₁（q－1）=3，d+b₁q（q－1）=4，d+b₁q²（q－1）=6，

即b₁（q－1）=3－d，b₁q（q－1）=4－d，b₁q²（q－1）=6－d，

根据题意知q≠1，以上三式对应相除，可得q=，q=，由=解得d=2；

则q==2，所以有d+q=2+2=4，故填答案：4．

点评：通过n的分类讨论以及数列{a_n+b_n}的前4项的确定，结合a₁+b₁=1与相应的关系式进行代数运算，并结合条件关系式的转化并建立相应的方程，从而得以确定d与q的值．其实，在确定a_n+b_n=2^n－1+2n－2时，分别利用等差数列与等比数列的函数性，直接得以确定a_n=2n－2，b_n=2^n－1，进而确定公差与公比的值，在解决小题时经常可以这样处理，节省时间，投机取巧．

思维视角二：公式应用

方法2：（对比系数法1）

解析：设等差数列{a_n}的公差为d，等比数列{b_n}的公比为q，根据题意知q≠1，

则等差数列{a_n}的前n项和公式为P_n=na₁+d=n²+（a₁－）n，

等比数列{b_n}的前n项和公式为Q_n==－qⁿ+，

依题意S_n=P_n+Q_n，即n²－n+2ⁿ－1=n²+（a₁－）n－qⁿ+，

通过对比系数可知，解得，所以有d+q=2+2=4，故填答案：4．

点评：根据等差数列与等比数列的前n项和公式建立相应的关系式，根据条件S_n=n²－n+2ⁿ－1，通过对比相应关系式中的系数关系建立对应的方程组，进而得以确定相关参数d与q的值．从数列求和公式角度入手进行对比系数法处理．

方法3：（对比系数法2）

解析：当n=1时，S₁=a₁+b₁=1－1+2－1=1；

当n≥2时，a_n+b_n=S_n－S_n－1=n²－n+2ⁿ－1－[（n－1）²－（n－1）+2^n－1－1]=2^n－1+2n－2；

上式也适合n=1的情形，所以a_n+b_n=2^n－1+2n－2，n∈N*，

又a_n+b_n=a₁+（n－1）d+b₁q^n－1=b₁q^n－1+dn+a₁－d，

通过对比系数可知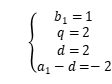，解得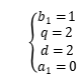，所以有d+q=2+2=4，故填答案：4．

点评：通过n的分类讨论来确定数列{a_n+b_n}的通项公式，分别结合等差数列与等比数列的通项公式的应用来建立相应的关系式，通过对比相应关系式中的系数关系建立对应的方程组，进而得以确定相关参数d与q的值．从数列通过公式角度入手进行对比系数法处理．

思维视角三：函数性质

方法4：（待定系数法）

解析：根据等差数列与等比数列的函数性质，

可知S_n=An²+Bn+C（qⁿ－1）=n²－n+2ⁿ－1，显然有A=1，B=－1，C=1，q=2，

而由A==1，解得d=2，所以有d+q=2+2=4，故填答案：4．

点评：根据等差数列与等比数列的函数性质，直接确定对应的前n项和公式的表达式，引入参数，根据条件S_n=n²－n+2ⁿ－1，通过对比相应关系式中的系数关系来确定相应的参数值，通过待定系数法的转化，进而得以确定相关参数d与q的值．待定系数法，抓住数列的函数性，引入参数，巧妙快捷．数列的函数性质法处理，也充分体现新课标数学高考的“多考思维，少考计算”的命题新理念，意在考查学生的分析、观察、归纳、猜想和逻辑推理能力等，充分体现学生思维能力的差异性，具有很好的选拔性与区分度．

通过“一题多解”，开阔解题思路，妙法顿生，培养学生的发散思维能力，激发学习的主动性、积极性、趣味性，全面提高知识水平和思维广阔性．

2．一题多变

一题多变是在教师精心安排下，在实际教学过程中，以一道典型例题为模板，在解决的基础上再从多角度、多方位、多层面等思维视角提出不同的问题，以进一步加深学生对知识的理解和掌握．一题多变能有效促进数学知识、思想方法和能力的融会贯通、举一反三、触类旁通，培养创新思维与创新意识，提升创新能力与核心素养．

例2．（2018年高考数学全国卷Ⅱ理科第12题）已知F₁，F₂是椭圆C：+=1（a>b>0）的左、右焦点，A是C的左顶点，点P在过A且斜率为的直线上，△PF₁F₂为等腰三角形，∠F₁F₂P=120º，则C的离心率为（）

A．                B．                C．                D．

分析：结合∠F₁F₂P=120º并利用三角形的性质来确定点P的坐标为P（2c，c），并结合题目条件确定点A的坐标，利用直线的斜率公式加以转化，整理得到a与c的关系式，进而得以求解椭圆的离心率．

解析：由于△PF₁F₂为等腰三角形，∠F₁F₂P=120º，可知F₂P=F₁F₂=2c，

结合图形可得P（2c，c），

而A（－a，0），则有k==，整理可得a=4c，

所以椭圆C的离心率为e==，故选择答案：D．

变式方向1：改变题目中的相关数据，难度相当Þ

【变式1】已知F₁，F₂是椭圆C：+=1（a>b>0）的左、右焦点，A是C的左顶点，点P在过A且斜率为的直线上，△PF₁F₂为等腰三角形，∠F₁F₂P=120º，则C的离心率为（）

A．                B．                C．                D．

解析：由于△PF₁F₂为等腰三角形，∠F₁F₂P=120º，可知F₂P=F₁F₂=2c，结合图形可得P（2c，c），而A（－a，0），则有k==，整理可得a=2c，所以椭圆C的离心率为e==，故选择答案：B．

变式方向2：改变圆锥曲线的类型，难度相当Þ

【变式2】已知F₁，F₂是双曲线C：－=1（a>0，b>0）的左、右焦点，A是C的左顶点，点P在过A且斜率为的直线上，△PF₁F₂为等腰三角形，∠F₁F₂P=120º，则C的离心率为（）

A．                B．2                C．                D．

解析：由于△PF₁F₂为等腰三角形，∠F₁F₂P=120º，可知F₂P=F₁F₂=2c，结合图形可得P（2c，c），而A（－a，0），则有k==，整理可得c=2a，所以双曲线C的离心率为e==2，故选择答案：B．

变式方向3：改变题目条件，难度相当Þ

【变式3】已知F₁，F₂是椭圆C：+=1（a>b>0）的左、右焦点，△PF₁F₂为等腰三角形，∠F₁F₂P=120º，若点P恰好在椭圆C上，则C的离心率为________．

解析：由于△PF₁F₂为等腰三角形，∠F₁F₂P=120º，可知F₂P=F₁F₂=2c，结合图形可得P（2c，c），而点P恰好在椭圆C上，则有+=1，结合b²=a²－c²，整理可得4c⁴－8a²c²+a⁴=0，则有4e⁴－8e²+1=0，解得e²=或e²=（由于0<e<1，舍去），由e²=可得e=（负值舍去），故填答案：．

通过“一题多变”，培养学生的转向机智及思维的应变性，实现提高发散思维的变通性．

“一题一课”教学，借助一题多解，一题多变等方式，合理达到一题一练一测一思一小结．以问题驱动为导向，教师体现主导作用加以合理引导，充分体现学生的主体地位，知识尽可能让学生回顾，思路尽可能让学生探寻，方法尽可能让学生寻找，变式尽可能让学生尝试，从而真正实现知识回顾问题化，思路探寻发散化，方法寻找多样化，变式尝试创新化，全面提升数学能力，提高思维品质，培养数学核心素养．