一体两翼：教学互融，素养进阶

宜兴市丁蜀高级中学   陈蓉

随着现代教育形势发展、新课程改革的推进，要求教师在教学过程中要切实改变传统的教学方法，构造“一体两翼”数学教学体系，即以打造优效课堂为主体，教法和学法为两翼，寓学法于教法之中，全面提高学生的数学素养。学习进阶理论指出，学生习得知识和技能的过程并非一蹴而就，需要教师为其设计合理的认知路径，搭建从低阶思维向高阶思维演进的脚手架，帮助学生个性化地实现素养进阶。具体落实在教学过程中，即将好教法变为学生的好学法、以学法定教法，从而做到既教知识、又教方法。 因此，探索学习方法是教师教学中的重要内容，从教师在“教”中充分体现学生的“学”，寻找数学生长的支点。

在高中阶段的数学教学中渗透学法指导，要注意提示隐含在教材中的数学思想方法，展现数学知识形成、发展的轨迹；要有意识地把思维过程中的方法比如比较与分类方法，分析与综合方法，归纳、演绎与类比的推理方法等结合具体的教学内容，深入浅出地教给学生，潜移默化地让学生获得良好学习方法的有益启示。下面就在课堂教学中如何开展教学学法的统一看几个课例的片段。

一、等差数列性质的教学

在等差数列性质的教学中，在介绍了用倒序相加法求等差数列前n项和的公式后，就提出如下问题让学生研讨：通过上述求和公式的推导，你们能发现等差数列有什么性质？

学生A：等差数列前n项中，只要

学生B：上述结论可推广到两边皆为项的情况，即若

老师：当两边个数不相等时，结论还成立吗？（学生小组讨论后认为不对）。

老师：上述结论的逆命题成立吗？（学生中一部分认为成立，一部分认为不一定，进行辩论）。

学生C：以两项为例， 

         若   

         故当；而当时，就不一定成立。

老师（简单小结）：通过研讨，我们不断把结论加以深入和一般化，这也是我们学习数学的一种重要方法。说明看书学习不能光知道结论，还要掌握某些重要公式定理的推导过程；更要善于观察思考，不断提出问题、深化问题，这样就能从中获得许多书中没有的知识。

老师：还有其他发现吗？

学生D：由上面的结论，还可以发现在等差数列中项与和的关系，可以用项来表示和：

还可以用和来表示项

 

老师：这位同学的想法很好。这个思想可以来解决下面的一类当？时，的最（或最小）的问题。如：已知数列是等差数列，且，问当？时，有最大值？

学生思考，解决问题。

整节课，师生之间、学生之间的思维活动都得到充分交流，相互启发、相互补充、相互评价，使人体会到一个问题的探究是怎样逐步深入地进行的。

表面看来十分简单的性质，运用科学的原理组织教学，就能引出十分丰富的内容，大大提高了学生分析、解决问题的能力。对于一些概念、习题，若能仔细推敲，深入钻研，把潜藏的基本思路、基本规律发掘出来，把教材的思维过程、教师的思维过程、学生的思维过程展示出来，就能从题海中跳出来，提高学生的数学思维素质。

二、正弦定理推导的教学

通过生活实例，引入正弦定理，以直角三角形为特例，先在直角三角形中试探发现成立，在几何画板中验证发现任何三角形都成立。

师：既然是定理，则需要证明，请同学们与小组共同探究正弦定理的证明。

探究方案：

直角三角形——已验证；锐角三角形——课堂探究；

钝角三角形——课后证明。

师：请你（某学生）到讲台上，讲讲你的证明思路？

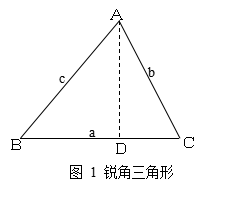
生：（走上讲台），设法将问题转化成直角三角形中的问题进行解决。通过作三角形的高，如图1作BC边上的高AD，则

，所以，同理可得

师：因为要证明的是一个等式，所以应从锐角三角形的条件出发，构造等量关系从而达到证明的目的。注意： 表示的几何意义是三角形同一边上的高不变。这是一个简捷的证明方法！（点明此证法的实质是找到一个可以作为证明基础的等量关系，为后续两种方法的提出做铺垫，同时适时对学生作出合情的评价。）

师：在三角形中还有哪些可以作为证明基础的等量关系呢？

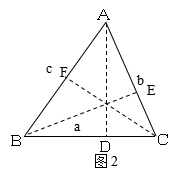学生七嘴八舌地说出一些等量关系，经讨论后确定如下一些与直角三角形有关的等量关系可能有利用价值：①三角形的面积不变；②三角形外接圆直径不变。在教师的建议下，学生分别利用这两种关系作为基础又得出了如下两种证法：

证法二：如图2，设AD、BE、CF分别是的三条高。则有：，，。                                        

∴

∴　

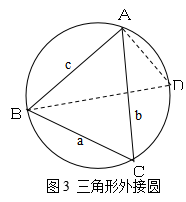
证法三：如图3，设是外接圆的直径，

则，

同理可证：

 

在证明正弦定理的同时，将两边及其夹角的三角形面积公式及一并牵出，使知识的产生自然合理。

师：前面我们学习了平面向量，能否运用向量的方法证明呢？

师：任意中，三个向量、、间有什么关系？

生：

师：正弦定理体现的是三角形中边角间的数量关系，如何由转化成数量关系？

生：利用向量的数量积运算可将向量关系转化成数量关系。

师：在两边同乘以向量,有,这里的向量可否任意？又如何选择向量?

生：因为两个垂直向量的数量积为0，可考虑让向量与三个向量中的一个向量（如向量）垂直，而且使三个项的关系式转化成两个项的关系式。

师：还是先研究锐角三角形的情形，按以上思路，请大家具体试一下，看还有什么问题？

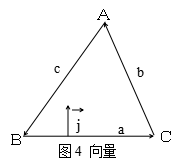教师参与学生的小组研究，同时引导学生注意两个向量的夹角，最后让学生通过小组代表作完成了如下证明。

证法四：如图4，设非零向量与向量垂直。

因为，所以

即

      

    所以，同理可得

师：能否简化证法四的过程？ 有什么几何意义？

（留有一定的时间给学生思考）

生：把移项可得，由向量数量积的几何意义可知与在方向上的投影相等。

生：我还有一种证法

师：请你到讲台来给大家讲一讲。（学生上台板书自己的证明方法。）

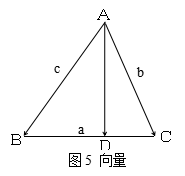证法五：如图5，作，则与在方向上的投影相等,即

  

故，同理可得 

师：利用向量在边上的高上的射影相等，证明了正弦定理，方法非常简捷明了！

（利用向量法来证明几何问题，学生相对比较生疏，不容易马上想出来，教师通过设计一些递进式的问题给予适当的启发引导，将很难想到的方法合理分解，有利于学生理解接受。）

整个过程让学生通过自主探索、合作交流，亲身经历了 “提出问题”——“研究特例”——“归纳猜想”——“实验探究”——“理论探究”——“解决问题”的历程，使学生成为正弦定理的“发现者”和“创造者”，切身感受了创造的苦和乐，从而达到了教学的目的。

从上面的两个课例可以看出：课堂教学中教师的主导和学生的主体作用主要体现在教师如何通过自己的教学，激发学生学习的自觉性和积极性，如何引导学生主动去观察、思考、探索，通过他们自己的努力去获取知识，使他们不但学会知识、运用知识，而且懂得如何去学，这是发挥教师的主导作用和学生的主体作用的根本所在。

   “一体两翼”数学教学体系逐渐产生出绵长不息的力量，学生感受到了蕴含于冰冷知识背后的火热思考。学习数学，欣赏数学，内化数学，让数学的生长力成为促进学生终身发展的进阶内驱力，最终让进阶数学植入生命的永恒。