评意隽永，引思精当

丁蜀高级中学       陈蓉，陈萍

高三数学二轮复习课中，试卷讲评是一种重要的课型，而在讲评中应充分遵循学生的思维，多从学生的角度去分析、去思考，笔者最近在一所学校听试卷讲评时有这样一道题：“关于的不等式的解集为A，若集合A中恰有两个整数，则实数的取值范围是      ”，老师在讲评这题时先向学生讲评了一个引例：“设集合中恰有两个整数，求实数的范围”。

教师分析：集合A中恰有两整数，等价于不等式中恰含有两个整数，即函数与轴两交点间含有两个整数点，因为函数图象的对称轴为，由对称性可知，只要即可，解得，再看本题与引例不同的是对称轴在移动，所以首先应突破此难点。由不等式的解集非空，则必须有，解得或。

当时，令，因为对称轴，且，所以整数点（4，0）在函数与轴两交点之间，由对称性可知只要，解得，同理当时，，只要，解得。由此可得实数的取值范围是或。

1、 引发的思考：

教师给出引例的目的是给学生有解题的思路，同样含参数的不等式，同样是含有两个整数，但将对称轴固定了，使学生入手易，所以平时在处理较难的题目时，不失为一种较好的处理手段；另外引例中利用对称轴固定，所以只需考虑离对称轴最近的第2、3两个点，充分用好数形结合思想；当然在引题中还可以考虑先画出函数的图象，然后画出的图象，只需考虑与的图象的交点以下部分恰含两个整数，因为，再结合图象得。

    2、进一步探究：

按照刚才对引例的思考，联想对本例的解法还可作这样的尝试，

因为，所以可化简为。

当时，化为，令，则即。作出及的图象，在两个图象的交点下方恰有两个整数。由图象可知当时，最小，当时，；当时，。

所以，即。

同理可解得当时，。所以实数的取值范围是或。

这一种解法是将变量分出，然后画出图象得出结果，方法较好，因为有一部分图象不随变量的变化而变化。如果想通过作出函数也可以根据图象解，但感觉差一点。

3、学生怎样解：

试卷讲评应是教师根据学生的错误，分析给学生听的，如果脱离了学生的实际，那么我们的讲评就显得是低效，本节课完后，我就和任课教师聊起了学生的解法，教师说学生好多是用设方程的两根为，则不等式的解集A中恰有两个整数，对应，即，解得或，错了。

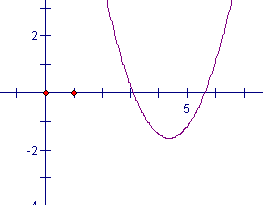
学生用这种方法解，那么我们的讲评为什么不从学生的想法开始呢？学生的解法错在那儿呢？带着这个问题，我就作了函数的图象，发现当时，这一点总在解集A内，但的条件是一个必要条件，不充分。如何调整？要用到估值思想，当时，方程的两根为，

也就是说不能保证在集合A中有两个整数点，而靠近这两根的整数点有，如果要保证在集合A中有两个整数点，则，解得，所以，同理可解另一范围为。

试题讲评，是大家经常在做的，但试题讲评能走多远，可能思考得不多，这儿想从这一题中得出，我们的试题讲评一要遵循学生的想法，先从学生的解法开始，帮助学生去分析错的原因、解法的不合理等，然后再指出如何优化，并且充分利用好数学思想，只有这样，我们的讲评效果才会越来越好。