

加入时间:2022-05-25
加入时间:2022-05-25
加入时间:2022-05-25
加入时间:2022-05-25
加入时间:2022-05-25

加入时间:2022-05-25

加入时间:2022-05-25
加入时间:2022-05-25
加入时间:2022-05-25

加入时间:2022-05-25

加入时间:2022-05-25
加入时间:2022-05-25
加入时间:2022-05-25
加入时间:2022-05-25

加入时间:2022-05-25
加入时间:2022-05-25
加入时间:2022-05-25
加入时间:2022-05-25
加入时间:2022-05-25

加入时间:2022-05-25
摘要:数学学科核心素养包括:数学抽象、逻辑推理、数学建模、直观想象、数学运算和数据分析,它们既相对独立,又相互交融,是一个有机的整体。数学运算是六大核心素养中非常重要的一部分,也是整个高中数学乃至大学数学中比较重要的一部分。它是指在明晰运算对象的基础上,依据运算法则解决数学问题的素养。主要包括:理解运算对象,掌握运算法则,探究运算思路,选择运算方法,设计运算程序,求得运算结果。
关键字:数学核心素养,数学运算,数学教学,高考
数学是研究数量关系和空间形式的一门科学,它源于对现实世界的抽象,基于抽象结构,通过符号运算,形式推理,模型建构等,理解和表达现实世界中事物的本质,关系和规律。数学教育承载着落实立德树人根本任务、发展素质教育的功能,由于传统应试教育的弊端越来越明显,让人们进一步认识到在核心素养背景下进行教学的重要性,通过创设合适的教学情境,启发学生思考,引导学生把握数学内容的本质,从而培育科学精神和创新意识。
核心素养的核心其实是深入回答“培养什么人,怎样培养人”,数学学科核心素养包括:数学抽象、逻辑推理、数学建模、直观想象、数学运算和数据分析,它们既相对独立,又相互交融,是一个有机的整体。
数学运算是六大核心素养中非常重要的一部分,也是以后学习和生活中比较重要的一部分。它是指在明晰运算对象的基础上,依据运算法则解决数学问题的素养。主要包括:理解运算对象,掌握运算法则,探究运算思路,选择运算方法,设计运算程序,求得运算结果。它是解决数学问题的基本手段,是演绎推理的重要形式,是计算机解决问题的基础。高中阶段数学学习任务繁重,在教学中,教师和学生都只注重思维能力的培养,进行题海战术,忽视了数学的运算的培养,很多时候,学生没考好也只是归结为计算出错,殊不知,数学运算涵盖特别多的方面,不仅仅是计算这一方面,它还与其他能力密切相关。
一、核心素养视角下培养高中生数学运算能力的重要性
1.帮助学生更好的理解知识内部的联系
根据皮亚杰的认知发展理论,认知结构的发展是一个连续建构的过程,每一阶段都有独特的结构,前一阶段是后一阶段的基础。虽然不同的人会以不同的发展速度经历这几个阶段,但是都不可能直接跳跃某一个阶段。纵观从小学到中学再到大学的数学运算,总是从低级到高级,从简单到复杂,从具体到抽象,有层次的发展起来的。
例1.已知点P![]() ,直线
,直线![]() ,如何求点P到直线
,如何求点P到直线![]() 的距离?
的距离?
![]()
![]()

![]()
![]()
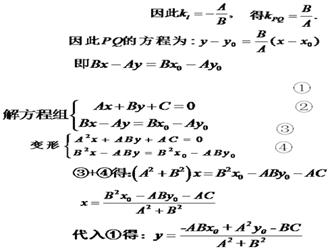
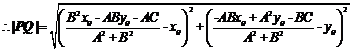 |
|||||
当A=0或B=0时,上述公式仍然成立。
点到直线的距离公式是平面几何中非常重要一个公式,它是直线方程的一个直接应用,推导这个公式的方法很多,第一种方法就是综合法—把点到直线的距离转化为两点间的距离,由两点间的距离公式得出结论,这种方法自然但是运算复杂。
方法二:从点P![]() 与直线
与直线![]() 上的任意一点M(x,y)构成的向量
上的任意一点M(x,y)构成的向量![]() 出发,通过构造与直线
出发,通过构造与直线![]() 垂直的单位向量
垂直的单位向量![]() ,得到向量
,得到向量![]() 在
在![]() 上的投影向量
上的投影向量![]() ,把点P到直线
,把点P到直线![]() 的距离转化为投影向量
的距离转化为投影向量![]() 的模,即
的模,即![]() ,从而求到点到直线的距离。这种方法是运用向量的投影和数量积公式运算进行推导,虽然运算量不大,但是需要有一定的整体观和构造技巧,包括与已知直线垂直的单位向量的选择,以及由向量及其投影的模表示点到直线的距离。
,从而求到点到直线的距离。这种方法是运用向量的投影和数量积公式运算进行推导,虽然运算量不大,但是需要有一定的整体观和构造技巧,包括与已知直线垂直的单位向量的选择,以及由向量及其投影的模表示点到直线的距离。
这两种方法的差异是显而易见的,第一种是典型的坐标法,完全通过代数运算,中间过程都是带字母系数的表达式,形式很复杂,得到最终的结果需要较强的数学运算能力,这对于提升学生的数学运算素养是有利的。第二种是典型的向量法,这种方法构造性强,需要较高的思维水平以及对向量的深入认识,但是运算比较简便,事半功倍。总之,这两种方法各有特点,在解决问题的过程中体现了知识之间不同的联系方式。
2.帮助培养学生好的数学学习习惯
由于高中阶段学业紧张,内容繁多,压力比较大,就会导致走入只重视思维能力训练的误区,忽视了数学运算的培养,而且很多学生也认为平日计算不正确没关系,只要考试的时候仔细点算出来就行,殊不知,冰冻三尺非一日之寒,没有平常的充足的运算训练很难在考试关头算出正确的答案,因而师生在平日的教学与学习中一定要充分认识到对于运算能力的重要性。
在刚刚落幕的2022年江苏高考,数学整体难度加大,考生普遍反应题目都很好入手,但是好难计算,在高考卷中出卷人罕见的在选择,填空,大题都设置了一道圆锥曲线,众所周知,圆锥曲线的学习是高中阶段的重点也是最令学生害怕的一部分,害怕的原因在于难算,有可能花费了时间最终也不得分。
例2:已知椭圆![]() ,C的上定点为A,两个焦点为
,C的上定点为A,两个焦点为![]() ,离心率为
,离心率为![]() ,过点
,过点![]() 且垂直于
且垂直于![]() 的直线与C交于D,E两点,
的直线与C交于D,E两点,![]() ,则
,则![]()
方法一:由![]() 得
得![]() ,
,![]() ,
,![]() ,又
,又![]() ,故DE是
,故DE是![]() 的垂直平分线,易证
的垂直平分线,易证![]() 和
和![]() 全等,原问题转化为求
全等,原问题转化为求![]() 的周长
的周长
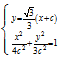 ,整理得
,整理得![]() ,设
,设![]() ,则
,则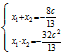 ,
,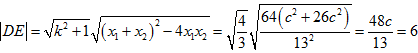 ,
,
![]() ,所以
,所以![]() 13.
13.
方法二:同方法一,原问题转化成转化为求![]() 的周长,且
的周长,且![]() ,
,![]() ,
,![]() ,
,![]() ,则
,则![]() ,
,![]() ,在
,在![]() 中,
中,![]() ,即
,即![]() ,即
,即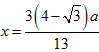 ,同理,在
,同理,在![]() 中,
中,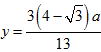 ,
,![]() ,故
,故![]() 13.
13.
方法三:设![]() ,则
,则![]() ,
,![]() ,
,![]() ,易知
,易知![]() ,
,![]() ,
,![]() ,
,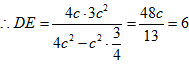 ,
,![]() ,
,![]() 。
。
这道高考题以椭圆为背景,知识点涵盖了初中学习的中垂线和全等三角形的知识,还考查了高中教材中椭圆的离心率,第一定义,焦点弦的弦长公式等知识,方法一是从弦长视角入手,这是解决解析几何的通性通法—通过联立直线与圆锥曲线方程再结合韦达定理,整个计算过程冗杂比较容易算错,方法二是从解三角形的角度入手,方法不咋常规,比较难想,而方法三则是从焦半径的角度思考,省时省力,正确率高。因而在平时的教学和学习中,师生不仅要重视通性通法,也要注意对二级结论的积累,多总结规律,降低计算出错的概率。
二、核心素养视角下培养高中生数学运算能力的策略
1.师生改变旧观念,重视数学运算
以往因为教学进度等多方面的原因,教师只是注重思维能力的培养,忽视了学生的运算能力的培养,比如在学习椭圆的标准方程这节新课时,不同建系方法都会导致标准方程不一样,以及对于等式![]() 的化简也只是提了化简过程并没有给学生充足的时间进行计算验证,这样根本起不到培养学生数学运算的能力的作用。因而,这就提醒教师在平日的教学过程中,务必要规范运算步骤和认真书写,对于一些看似简单地式子,法则等一定要仔细对待,强调解题步骤,分析运算过程,规范解题,这样才能提高解题速度和正确率。
的化简也只是提了化简过程并没有给学生充足的时间进行计算验证,这样根本起不到培养学生数学运算的能力的作用。因而,这就提醒教师在平日的教学过程中,务必要规范运算步骤和认真书写,对于一些看似简单地式子,法则等一定要仔细对待,强调解题步骤,分析运算过程,规范解题,这样才能提高解题速度和正确率。
2.夯实基础知识,力争“拾级而上”
对于数学知识的正确理解是运算的正确的前提条件,因而在平日的教学中,教师一定要重视基础知识的教学,知识的产生,发展过程讲授清楚,这样既能提高课堂的效率,也可以提升学生的能力。比如,在向量的数量积这节课中,学生对于![]() 不成立的原因不清楚。
不成立的原因不清楚。
3.防止思维定势,实现“移花接木”
所谓思维定势,是由先前的活动而造成的一种对活动的特殊的心理准备状态,或活动的倾向性,它对于数学解题的影响利弊共存,弊端是束缚了思考的空间,有可能大大降低了新型题目的解题的速度,比如今年高考多选12题,已知函数![]() 及其导函数
及其导函数![]() 的定义域均为R,记
的定义域均为R,记![]() ,若
,若![]() 均为偶函数,则
均为偶函数,则![]()
![]()
![]()
![]()
方法一:设![]() ,则
,则![]() ,
,![]() 为偶函数,所以
为偶函数,所以![]() ,则
,则![]() ,则
,则![]() 为偶函数,所以
为偶函数,所以![]() 也满足题目要求,而c是任意的,所以
也满足题目要求,而c是任意的,所以![]() 不确定,A错误。
不确定,A错误。
![]() ,所以
,所以![]() ,所以等式两边取导数也相等,即
,所以等式两边取导数也相等,即![]() ,则
,则![]() ,又
,又![]() ,则
,则![]() ,则
,则![]() ,B正确。
,B正确。
![]() ,所以
,所以![]() ,C正确。
,C正确。
由B得![]() ,所以
,所以![]() ,D错误。
,D错误。
方法二:设![]() ,题目迎刃而解。
,题目迎刃而解。
一题多解是破除思维定势障碍的主要方式,平时在训练和考试时,一定要注重小题小做,对于选择题和填空题,可以采用直接求解法,特殊值,特殊位置,特殊点,特殊模型等。
总之,师生对于运算能力的培养任重而道远,必须深入理解数学核心素养的内涵,探究数学核心素养的培养路径,使得核心素养成为教师教学工作的指路明灯,成为学生成长的DNA,引领高中教育深化改革,从“知识本位”时代走向“核心素养”时代。
参考文献:1.吴晓红,谢海燕.基于学科核心素养的数学教学课例研究,2019
2.陈玉荣,核心素养视域下高中数学教学中学生运算能力培养的策略分析,新课程,2020