摘要：数学思想方法是人们根据具体的数学内容总结出来对数学知识的本质认识。转化思想就是把一种数学问题转化成另一种数学问题进行换位思考，从而使问题得到合理有效地解决的方法。本文尝试通过实例从转化思想运用的原则这一角度阐述高中数学教学中转化思想的运用.

关键词：高中数学，转化思想，运用原则，问题转化

当我们在解决数学问题的时候，或多或少都会遇到一些难以直接解答出来的问题，因此，我们要运用恰当的数学方法对问题进行有目的地转化，将原有的问题转化成一个新的问题，以新问题的解决为目标，达到解决原有问题的目的，这种思想方法就是转化思想方法。其核心是用不断变化的观点去对你所要解决问题进行变形，通过变形把你需要解决的问题，转化为某些已经解决的问题，从而使原有的问题得以解决。

转化思想在高中数学各部分知识中无处不见，它对强化学生解决问题的应变能力，提高学生思维能力，提高学生解题技巧都起到很大的作用，要实施好转化，必须遵循一定的原则，使转化有效。

一、简单熟悉化原则

这是数学教学中最常见的解题方法之一，你需要学生拥有一定的数学基础知识、技能与方法，因为它既是我们解决一些基本问题所必须掌握的基本方法，又是解决那些复杂问题所需的重要方法，也是将陌生的、复杂的问题变为熟悉的、简单的问题的思维过程。

例1 设，求函数的值域.

分析：本题中的函数是一个复合函数，我们可以通过换元把它转化成我们熟悉的一元二次函数，通过求解一元二次函数的值域得到原函数的值域，需要注意的是换元之后自变量的范围改变。

解：令（），则，

∴当时，函数取得最小值，

当时，函数取得最大值，

∴函数的值域为.

例2 已知在数列中，，，求这个数列的通项公式.

分析：通过观察我们发现该数列不是我们熟悉的等差数列或者等比数列，但是我们可以通过构造一个新的数列，使得新数列成等差或者等比从而去求解通项公式。

解：递推公式可以转化为

      即，得到

      故递推公式为

      令，则，且

      ∴数列是以，为公比的等比数列，

      则

∴.

二、直观和谐化原则

直观化原则就是将相对笼统的问题换一个思考的角度，变成可以直面的问题，这样解决起来也比较方便；和谐化原则就是转化问题的已知条件或结论，让它看上去更加符合数与形内部所表现出来的和谐形式，在数学解题中我们会遇到很多这类的问题。例如，在中，证明，等式左边是三角形边与角的关系式，右边是三角形边的关系式。此时根据式中半角我们联想到半角公式和余弦定理，可以把左边转化成关于三边的关系式，于是整式也就全部统一成边的形式，从而可以证明左右相等，体现和谐化原则。在整个转化过程中，需要符合思维的规律。

例3 在中，角对应的边分别为，，求角的大小。

分析：本题体现出的是三角形面积与向量的关系，此时我们联想到在学习正弦定理的时候利用向量的方法证明了正弦定理公式并且推导得出了三角形的面积求解公式，所以我们要把式中的数量统一成边和角，再将边转化成角从而求得未知角的大小。

解：由得 

       因为 所以，即

       又因为，所以.

三、正难则反原则

正难则反原则是当你正面解决问题有困难的时候，试着从反面去考虑问题，从反面去探究，使问题得到解决。这也是数学解题中经常出现的方法，例如：在解题中碰到如果要证明不等式，不妨先假设，然后根据假设和不等式的一些性质，推导出与题目已知相矛盾的地方，从而否定假设，得到我们正确的结论。在证明题中碰到要证明的不等式中含有“至多”、“至少”、“所有”、“都是”、“不都”、“存在”、“任意”、“唯一”等全称量词或存在性量词，且从正面的角度难以找到解题的突破口时，我们不妨转变一下看问题的角度，用反证法往往立竿见影。通过对于这一原则的理解和应用，还能达到锻炼学生逆向思维能力的目的。

例4 判断命题“若，则”的真假。 

分析：要说明此命题是假命题，直接举反例否定显然比正面理论说明更直接有效，可取，，则，但，，所以命题是假命题。

例5 如图，设SA、SB是圆锥SO的两条母线，O是底面圆心，C是SB上一点.求证：AC与平面SOB不垂直.

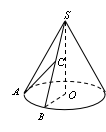分析:结论是“不垂直”，呈“否定性”，考虑使用反证法，即假设“垂直”后再导出矛盾后，再肯定“不垂直”.

证明:假设AC⊥平面SOB，

∵ 直线SO在平面SOB内，   ∴ AC⊥SO，

∵ SO⊥底面圆O，     ∴ SO⊥AB，

∴ SO⊥平面SAB，    ∴平面SAB∥底面圆O，

这显然出现矛盾，所以假设不成立，

即AC与平面SOB不垂直.

例6 若下列方程：，，至少有一个方程有实根.试求实数的取值范围。

分析：三个方程至少有一个方程有实根的反面情况仅有一种：三个方程均没有实根。先求出反面情况时的范围，再求所得范围的补集就是正面情况的答案。

解：设三个方程均无实根，则有：，

解得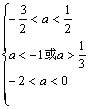，即

所以当或时，三个方程至少有一个方程有实根.

以上的实例说明“正难则反”是一种通过转化的方式更好解决问题的策略，它不仅能开拓解题思路，打破思维定势，还能简化运算过程，提高解题速度，是突破传统框架产生新思路的源泉。

高中生面对高考等压力的影响，解题方式往往是单一且不会变通，因而不能真正地理解并运用所学知识。因此，在教学过程中，教师要利用学生已有的基础知识，引导学生进一步的思考，这需要教师持续地培养学生积极学习的能力，并在教学实践中融入转化思想去探寻解决问题的思路与方法，使其成为学生分析和解决问题的重要工具。总而言之，教师应该根据教材的内容，化隐为显，掌握转化与化归的方法，采用循序渐进的教学原则，结合不同阶段、不同学习内容，不断地渗透转化思想，最终达到学生可以自主地通过转化思想来解决困难的一个境界。