【摘要】选取了数学思想中的一种——分类思想进行了具体的研究，具体论述了分类数学思想的的简化技巧以及具体举例说明高中常见的运用数学简化分类思想的例题，最后做出了总结。本文尝试通过实例从分类讨论思想运用的原则这一角度阐述高中数学教学中分类讨论思想的运用.

【关键词】分类；数学思想；解题；策略

随着新课程的实施，数学思想方法逐步引起重视。素质教育也提倡教学过程应当注意学生数学能力的发展和数学素养的提高。但是根据事实情况，教师自身对于数学思想方法的认识还不是很到位。受传统教育观念的影响，教师在实际教学中仍然比较偏重课本知识的传授，而忽视了教学过程的体验以及数学思想的渗透，以至于学生对知识的本质内涵不是很清楚，不利于学生对知识的整体构建。所以，要渗透数学思想、发展素质教育，从教育者的角度来看，第一步就是要提高我国教师的教育观。

对于学生来说，因为年龄或思维模式的原因，学生对数学思想的感悟也存在问题，在分类讨论中常常会有一些误区，比如：在问题分析中缺乏分类讨论的意识；分类讨论时具有盲目性；分类讨论有较强的主观性等。在中学尤其是高中阶段的分类讨论中，学生可能觉得有些题目较繁杂、层次很多，不容易求得解，其实在分类讨论中我们除了按常规思路来，也可以稍稍改变一下思路，合理分类，适当运用一些小技巧，可能解决此类问题的过程就大不一样了。

一、合理分类

例1.已知，，，，求函数的定义域。

解：首先函数的定义域要满足，即，所以，又，，，即；接下来就是对进行分类讨论：

①若时，则；

②若时，还需要对、、再进行讨论：

ⅰ当时，；

ⅱ当时，；

ⅲ当时，，当时，；当时，。

分析：这道题有多层次，需要分类中再分类。不等式有两分类方法，先讨论，再讨论比较容易；如果先讨论，再讨论则相当麻烦，而且容易发生分类混乱。

因此对于未知数较多，多层次的分类讨论题，选择合理的分类方法十分重要，这样可以有效地优化解题的思路，完整的解答出一道看上去复杂的问题。

二、整体处理

例2.设，在复数集中，解方程。

分析：解决此题可能最初想到的思路就是设或，然后再带入方程进行多层次的讨论，十分复杂。但是我们从整体上观察，对进行整体处理，可以大大简化讨论。

解：，由已知得：为实数或者纯虚数。

①若为实数，则，（负数舍去），

②若为纯虚数，设则有，

，或

因此，综上：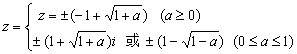

整体处理的方法是将原有的结构变换成一种新的整体，从而避开了复杂的讨论，简化了分类。不过可能对很多高中生来说都有困难，把什么量看成整体是不容易发现的，但是我们在遇到此类问题时，可以稍微往这上面想一想，仔细观察已知条件的特点，看是否能运用整体处理的思想来大大简化分类讨论的过程。

三、变换主元

例3.已知为正整数，当取何值时，方程的根至少有一个为整数？

分析：常规思路是，先求出方程的根，再对参数进行分类讨论，找出满足条件的值，但是由于“搜索范围”很大，讨论会十分繁琐，而且容易遗漏。但是如果换一下思路，改变一下主元，即对换原方程和的地位，把看作“主元”，用来表示，则将缩小讨论的范围，使讨论简化。

解：整理原方程得：，因为不满足方程，所以可以化成，又为正整数，，即，，

因此的取值只能有四种情况，即：

①，此时；②时；③时；④时。

所以，满足题意的是或者。

由此可见，在有不止一个未知数的代数问题里，有时候转变一下看问题的思路，变化一下“主元”，就可以很巧妙的避开复杂的讨论。

四、数形结合

数学的美妙不仅仅在于数字的变换，数学中的图形也十分有魅力。数形结合也是常用的数学思想方法之一，是指把数量间的关系通过图形表示分析出来，图形的好处是可以直观形象地反映出各数量间之间的关系，如果我们能够适当的运用数形结合的方法在分类讨论的过程中，其实也是可以使讨论简便的。

例4.，若，求实数的取值范围。

解析：通常很多同学的思路会由得到，接着就转化为定区间上一元二次方程有解的问题，又是一场繁杂的分类讨论。这时候，我们可以换一种思路，有没有简单一点的方法呢？再研究题目，我们发现集合是有几何意义的，集合表示的是抛物线上的点集，集合表示的是一条线段上所有点的集合，又要，其几何意义就是两个图形要有交点。明确了这一点之后，我们接下来就可以求解了：根据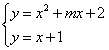得到，，             

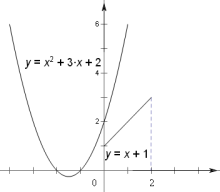
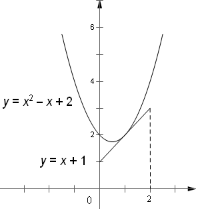
图4                                        图5

即或，又检验得时（图4），两图形明显没有交点，故舍去。

当时（图5），抛物线为，此时与线段相切，且顶点的纵坐标为，又因为抛物线过一定点，

或，又检验发现，时，两图形没有交点，

综上：

因此，我们说数学思想不是独立的、一成不变的，往往他们之间是相通的，有时候常常会起到意想不到的作用，在进行运用分类思想解决问题时，当某道题题目几何意义很明显的时候，我们就可以考虑是否可以跟数形结合思想结合起来用，以达到简便讨论的效果。

课堂教学是实施素质教育的主渠道，所谓“授人以鱼，不如授人以渔。”只有真正改善课堂教学的内容跟讲授形式，才能提高学生的课堂效率，也才能为学生思维的发展创造一个良好的外部环境。只有使学生掌握了数学方法，了解数学理念，形成数学思想，才能受益终生。巧妙运用数学思想往往可以使运算简便、推理灵活,解决各种常规的和非常规的数学问题。因此在进行分类讨论思想方法的教学时,应该结合中小学生的思维特点及他们的实际生活经验,用易于理解和掌握的教学方式,教授他们相关的解题策略，使学生形成正确的数学观和良好的数学意识。希望学生和老师都能共同努力，学好数学，把握住数学的精髓。

[1]刘江华.分类讨论思想在高一数学教学中逐步渗透的实践研究.[D].湖北师范大学2013.

[2]赵海霞.分类讨论——实现问题转化的重要思想方法[J].读与写(教育教学刊).2010年05期.

[3]王燕,刘相书,刘鑫.全面点击分类讨论法[J].数学教学通讯.2010年16期.

[4]徐望斌.对解题教学中分类讨论思想方法的探讨[J].湖北师范学院学报（自然科学）.2005年4月.

[5]罗树全.对数学新课程中分类讨论思想的再认识[J].教育实践与研究.2010年06期.

[6]赵建勋.简化分类讨论的策略[J].中学生数学.2012年2月