关于“等差数列前项和公式”这一节内容的教学设计，很多刊物给出了很多种各色各样不同的情境创设、不同的公式推导方案，并就此进行了评析和反思，给我带来了许多启发。前一段时间我有幸去江苏省常州高级中学参加了江苏省高中青年数学教师优秀课观摩活动，观摩了很多优秀青年教师以及一些专家的课堂，尤其是江苏省宜兴中学的王震老师展示的课堂让我受益颇深。

下面是王震老师推导“等差数列的前项和公式”的教学片段

《问题情境》高斯“神速求和”的故事

高斯出生于一个工匠家庭，幼时家境贫困，但聪敏异常。上小学四年级时，一次老师布置了一道数学习题：“把从1到100的自然数加起来，和是多少？”年仅10岁的高斯略加思索就得到答案5050，这使老师非常吃惊。

问题1：老师布置的题目从数列角度看是一个什么类型的问题？

高斯是用什么方法快速算出答案的？

学生1：一个等差数列求前100项和     

学生2：首尾配对     

教师：同学们能利用高斯加法解决了求和问题，那其实高斯用了等差数列的什么性质？

学生3：若，则

教师继续追问：有什么问题或者困惑要和大家探讨一下吗？

学生4：项数为偶数时，我们可以两两配对，但当项数变为奇数该怎么处理？

问题2：:你们能计算吗？

学生给出了不同的解决办法：

问题3：如何求

学生5：需要分类讨论。若是偶数，我们仍可以利用高斯加法来计算，与首末等距离的两项的和都等于，共有个.若是奇数，除去最后位置的数外，其余个数，与首末等距离的两项和都等于，共有个.

当为偶数时，

当为奇数时，   

综上：

教师：我们发现，不管是奇数还是偶数，结果都是一样的。

能不能不用分类讨论的方法，解决这个问题呢？

学生6：在前面求和过程中，运用了下标和性质进行首尾配对，我们可以直接将这个数列倒过来写一遍，从而左右分别相加。

    ①

   ②

由①+②得，

教师：非常好，这位同学的方法就是倒序相加求和法，通过倒序相加，能将复杂的求和问题转化为简单的求和。那是一个特殊等差数列（公差和首项均为1）求和问题，数学的学习大多要经历从特殊到一般的过程，推导出具有普遍性、一般性的等差数列求和公式才是这节课的主要目标！

问题4：一般地，如何求等差数列的前项和？（学生自主探究推导出前项和公式）

等差数列首项为，公差为

  则     ①

   ②

由①+②得，

评析  如何基于高斯神速求和故事引出求一般等差数列的前项和公式，很多教师为了能够顺利完成公式推导教学，在引入高斯求和后直接向学生抛出“倒序相加法”。但这样的“告知”无疑脱离了学生的思维发展实际，公式的探究过程就变成了灌输的过程。从接受式学习的角度来说，学生对“倒序相加”是非常容易理解和接受的。但从探究式学习的角度来看，教材的设计意图就没能实现，用高斯算法引入的思维价值没有恰当地发挥作用，只是为了引入而引入，更是违背了“数学是自然的”教学宗旨。但王老师的教学设计以一连串的问题式探究为主，让学生自己计算，，直到，让学生在自主探究的过程中发现问题，从而解决问题。从项数是偶数时利用首尾配对，到项数变为奇数时，求和遇到了阻碍，发现需要奇偶性分类讨论去进行求和，再到一步一步得到倒序相加求和，这一连串的方法都是让学生从已有的知识出发进行探索，尝试了原有方法解决的可能性，并在此基础上再进行探索研究，所学知识进行了一次崭新的整理，从中发现出一些有价值的东西，并应用于新的知识的探求，因此探究过程更加自然流畅。这样一来，不但启发了学生掌握从特殊到一般的数学研究方法，发展了探究事物的能力，拓宽了理性思维，提高思维品质；而且学生还深切感受到成功的喜悦，培养了学生的自信，逐步形成勇于探索的学习方式。

在学生们利用倒序求和的方法推导出等差数列的前项和公式后，王老师又展现了这样一个故事：

链接：成书于公元5世纪的《张丘建算经》中有这样一个问题：

今有女不善织，日减功迟，初日织五尺，末日织一尺，近三十日织讫. 问织几何？

（通过学生读题，将其转化为等差数列求和的数学问题）

告知原书解法：并初、末日织布数，半之，余以乘织讫日数，即得！

另有一女善织，日益功疾，初日织一尺，末日织五尺，近三十日织讫. 则两女织布数无异！

根据原书中假设的两个情境，引导学生得出:

从而得到:

评析  王老师设计的这一环节，用幽默的语言阐述了《张丘建算经》中织女织布的故事，学生反应热烈，都投入到这个情境中去，一起去揭秘两织女的织布数。这样的设计，揭示原书中所给出解法背后的思想方法，在此过程中一方面，《张丘建算经》成书于公元5世纪，比高斯想出方法时早了1000多年，充分让学生体会到古代数学家的博大智慧，为实现中国民族的伟大复兴作出贡献。另一方面，通过题中假设的两个情境，能让学生更加真实地体会倒序相加法求和的思想。其实数列的历史源远流长，在中国古代文献中，记载了许多有趣的数列问题。出土的春秋至战国时代楚国的铜环权，其重量大致都按等差或等比数列配置。等差数列求和问题最早见于约成书于公元前1世纪的《九章算术》，其中的衰分章、均输章、盈不足章中就有许多关于等差数列的问题。值得我们骄傲的是，刘徽在《九章算术注》中创造了等差数列的求和公式和两个通项公式。这一创举比其他国家至少领先300年，可以说刘徽在中国数学史上的贡献是空前巨大的！此外《孙子算经》《前汉书》《旧唐书》《张丘建算经》中也记载了很多有趣的数列问题，

   在这个信息发达的时代，查查资料，拼凑剪贴，备出一节课来不是一件很难的事，凭已有的功底应付平常的教学也似乎是绰绰有余，更何况现在提倡的都是集体备课。而恰恰是这样的情形，造成了我们老师另一方面的“惰性”，就是没了自己，没了独立思考，没了个性化的教学设计，也就没了个性化的课堂。很多课听下来，千篇一律。试想一下，老师、课堂都像流水线上生产产品似的，学生的个性化又从何谈起呢？因此在借他山之石后，自己也要经过一番打磨，方能攻玉，我们这些青年老师更要能平心静气地坐下来，潜心会文，加以咀嚼、内化，才会上出精彩的有个性的课。

接着王老师提出了问题5，

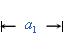
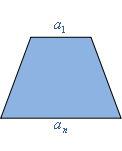
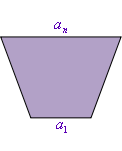
问题5：还记得梯形面积公式是如何推导的吗?它与等差数列前项和公式有联系吗?

学生7: 在梯形边上倒放一个全等的梯形，把梯形补成平行四边形．

学生8: 还可以把梯形分割成一个平行四边形和一个三角形．

梯形的面积公式还可以帮助我们记忆等差数列前项和的公式．

评析  在以下教学片断中，我认为王老师的处理是比较成功的，利用图形的“补”和“割”，推导出梯形的面积公式，并引导学生通过探究可用图形来解释倒序相加法，思考并理解等差数列前项和公式的几何解释，加深对求和公式的理解与记忆，同时也启发我们，该如何帮助学生建立起公式与图形之间的联系。

其实很多教师在得到公式后就直接进入公式的应用环节。在他们看来，让学生知道公式是怎么来的，有什么用，及如何用就可以了，并不关注公式的几何意义；知道不知道公式的几何意义，并不影响学生对公式的正确应用。或者说，他们并没有意识到公式几何意义的作用。事实上，明确公式的几何意义，有助于学生深入理解公式，在理解的基础上记忆公式，而不是机械地去记忆公式。等差数列前项公式其实有简单而形象的几何意义，可以沟通代数与几何的联系，并帮助学生从整体上把握公式。

《普通高中数学课程标准》中指出：“在教学中，教师应根据高中数学课程的理念和目标，学生的认知特征和数学的特点，积极探索适合高中学生数学学习的教学方式.”意思就是我们在教学时，要时刻不忘学生，时刻琢磨着是不是“适合”学生。因此，在教学的过程中，如何将教材呈现的知识进行再创造，通过问题式探究激发学生的主观能动性，激发学生的思维，在学习探究的过程中积累经验，获得快乐，而不是单一无趣的知识点和公式等等。对于学生来讲，某个知识点经过一段时间或许会遗忘，但是这种思想方法，课堂上生动的情境会让他终生难忘。这些经验为他以后不光是学习、生活、工作都能让他以此借鉴，发现问题、提出问题、研究问题、解决问题。其实这样的课例比比皆是，关键是要做个有心之人，在学习中不断成长，在成长中不断学习。